2.4 Distance measures
In this section we summarize various distance measures that are defined in an arbitrary spacetime. Some
of them are directly related to observable quantities with relevance for lensing. The material of this section
makes use of the results on infinitesimally thin bundles which are summarized in Section 2.3. All of the
distance measures to be discussed refer to a past-oriented lightlike geodesic  from an observation event
from an observation event
 to an emission event
to an emission event  (see Figure 4). Some of them depend on the 4-velocity
(see Figure 4). Some of them depend on the 4-velocity  of the observer
at
of the observer
at  and/or on the 4-velocity
and/or on the 4-velocity  of the light source at
of the light source at  . If a vector field
. If a vector field  with
with
 is distinguished on
is distinguished on  , we can choose for the observer an integral curve
of
, we can choose for the observer an integral curve
of  and for the light sources all other integral curves of
and for the light sources all other integral curves of  . Then each of the distance
measures becomes a function of the observational coordinates
. Then each of the distance
measures becomes a function of the observational coordinates  (recall Section 2.1).
(recall Section 2.1).
Affine distance.
There is a unique affine parametrization  for each lightlike geodesic through the observation
event
for each lightlike geodesic through the observation
event  such that
such that  and
and  . Then the affine parameter
. Then the affine parameter  itself
can be viewed as a distance measure. This affine distance has the desirable features that it
increases monotonously along each ray and that it coincides in an infinitesimal neighborhood
of
itself
can be viewed as a distance measure. This affine distance has the desirable features that it
increases monotonously along each ray and that it coincides in an infinitesimal neighborhood
of  with Euclidean distance in the rest system of
with Euclidean distance in the rest system of  . The affine distance depends on
the 4-velocity
. The affine distance depends on
the 4-velocity  of the observer but not on the 4-velocity
of the observer but not on the 4-velocity  of the light source. It is a
mathematically very convenient notion, but it is not an observable. (It can be operationally realized in
terms of an observer field whose 4-velocities are parallel along the ray. Then the affine distance
results by integration if each observer measures the length of an infinitesimally short part of the
ray in his rest system. However, in view of astronomical situations this is a purely theoretical
construction.) The notion of affine distance was introduced by Kermack, McCrea, and Whittaker [179
of the light source. It is a
mathematically very convenient notion, but it is not an observable. (It can be operationally realized in
terms of an observer field whose 4-velocities are parallel along the ray. Then the affine distance
results by integration if each observer measures the length of an infinitesimally short part of the
ray in his rest system. However, in view of astronomical situations this is a purely theoretical
construction.) The notion of affine distance was introduced by Kermack, McCrea, and Whittaker [179 ].
].
Travel time.
As an alternative distance measure one can use the travel time. This requires the choice of a time function,
i.e., of a function  that slices the spacetime into spacelike hypersurfaces
that slices the spacetime into spacelike hypersurfaces  . (Such a time
function globally exists if and only if the spacetime is stably causal; see, e.g., [153
. (Such a time
function globally exists if and only if the spacetime is stably causal; see, e.g., [153 ], p. 198.) The travel time
is equal to
], p. 198.) The travel time
is equal to  , for each
, for each  on the past light cone of
on the past light cone of  . In other words, the intersection of
the light cone with a hypersurface
. In other words, the intersection of
the light cone with a hypersurface  determines events of equal travel time; we call these
intersections “instantaneous wave fronts” (recall Section 2.2). Examples of instantaneous wave fronts are
shown in Figures 13, 18, 19, 27, and 28. The travel time increases monotonously along each ray. Clearly, it
depends neither on the 4-velocity
determines events of equal travel time; we call these
intersections “instantaneous wave fronts” (recall Section 2.2). Examples of instantaneous wave fronts are
shown in Figures 13, 18, 19, 27, and 28. The travel time increases monotonously along each ray. Clearly, it
depends neither on the 4-velocity  of the observer nor on the 4-velocity
of the observer nor on the 4-velocity  of the light
source. Note that the travel time has a unique value at each point of
of the light
source. Note that the travel time has a unique value at each point of  ’s past light cone,
even at events that can be reached by two different rays from
’s past light cone,
even at events that can be reached by two different rays from  . Near
. Near  the travel time
coincides with Euclidean distance in the observer’s rest system only if
the travel time
coincides with Euclidean distance in the observer’s rest system only if  is perpendicular to
the hypersurface
is perpendicular to
the hypersurface  with
with  . (The latter equation is true if along the
observer’s world line the time function
. (The latter equation is true if along the
observer’s world line the time function  coincides with proper time.) The travel time is not
directly observable. However, travel time differences are observable in multiple-imaging situations
if the intrinsic luminosity of the light source is time-dependent. To illustrate this, think of a
light source that flashes at a particular instant. If the flash reaches the observer’s wordline
along two different rays, the proper time difference
coincides with proper time.) The travel time is not
directly observable. However, travel time differences are observable in multiple-imaging situations
if the intrinsic luminosity of the light source is time-dependent. To illustrate this, think of a
light source that flashes at a particular instant. If the flash reaches the observer’s wordline
along two different rays, the proper time difference  of the two arrival events is directly
measurable. For a time function
of the two arrival events is directly
measurable. For a time function  that along the observer’s worldline coincides with proper time,
this observed time delay
that along the observer’s worldline coincides with proper time,
this observed time delay  gives the difference in travel time for the two rays. In view of
applications, the measurement of time delays is of great relevance for quasar lensing. For the double
quasar 0957+561 the observed time delay
gives the difference in travel time for the two rays. In view of
applications, the measurement of time delays is of great relevance for quasar lensing. For the double
quasar 0957+561 the observed time delay  is about 417 days (see, e.g., [275
is about 417 days (see, e.g., [275 ], p. 149).
], p. 149).
Redshift.
In cosmology it is common to use the redshift as a distance measure. For assigning a redshift
to a lightlike geodesic  that connects the observation event
that connects the observation event  on the worldline
on the worldline  of the observer with the emission event
of the observer with the emission event  on the worldline
on the worldline  of the light source, one
considers a neighboring lightlike geodesic that meets
of the light source, one
considers a neighboring lightlike geodesic that meets  at a proper time interval
at a proper time interval  from
from  and
and  at a proper time interval
at a proper time interval  from
from  . The redshift
. The redshift  is defined as
is defined as
If  is affinely parametrized with
is affinely parametrized with  and
and  , one finds that
, one finds that  is given by
This general redshift formula is due to Kermack, McCrea, and Whittaker [179]. Their proof is based on the
fact that
is given by
This general redshift formula is due to Kermack, McCrea, and Whittaker [179]. Their proof is based on the
fact that  is a constant for all Jacobi fields
is a constant for all Jacobi fields  that connect
that connect  with an infinitesimally
neighboring lightlike geodesic. The same proof can be found, in a more elegant form, in [41] and in [311
with an infinitesimally
neighboring lightlike geodesic. The same proof can be found, in a more elegant form, in [41] and in [311 ],
p. 109. An alternative proof, based on variational methods, was given by Schrödinger [299]. Equation (37)
is in agreement with the Hamilton formalism for photons. Clearly, the redshift depends on the 4-velocity
],
p. 109. An alternative proof, based on variational methods, was given by Schrödinger [299]. Equation (37)
is in agreement with the Hamilton formalism for photons. Clearly, the redshift depends on the 4-velocity
 of the observer and on the 4-velocity
of the observer and on the 4-velocity  of the light source. If a vector field
of the light source. If a vector field  with
with
 has been distinguished on
has been distinguished on  , we may choose one integral curve of
, we may choose one integral curve of  as the
observer and all other integral curves of
as the
observer and all other integral curves of  as the light sources. Then the redshift becomes a
function of the observational coordinates
as the light sources. Then the redshift becomes a
function of the observational coordinates  . For
. For  , the redshift goes to 0,
with a (generalized) Hubble parameter
, the redshift goes to 0,
with a (generalized) Hubble parameter  that depends on spatial direction and on time. For
criteria that
that depends on spatial direction and on time. For
criteria that  and the higher-order coefficients are independent of
and the higher-order coefficients are independent of  and
and  (see [151]). If the
redshift is known for one observer field
(see [151]). If the
redshift is known for one observer field  , it can be calculated for any other
, it can be calculated for any other  , according to
Equation (37), just by adding the usual special-relativistic Doppler factors. Note that if
, according to
Equation (37), just by adding the usual special-relativistic Doppler factors. Note that if  is given, the
redshift can be made to zero along any one ray
is given, the
redshift can be made to zero along any one ray  from
from  by choosing the 4-velocities
by choosing the 4-velocities  appropriately. This shows that
appropriately. This shows that  is a reasonable distance measure only for special situations, e.g., in
cosmological models with
is a reasonable distance measure only for special situations, e.g., in
cosmological models with  denoting the mean flow of luminous matter (“Hubble flow”). In any case, the
redshift is directly observable if the light source emits identifiable spectral lines. For the calculation of
Sagnac-like effects, the redshift formula (37) can be evaluated piecewise along broken lightlike
geodesics [23].
denoting the mean flow of luminous matter (“Hubble flow”). In any case, the
redshift is directly observable if the light source emits identifiable spectral lines. For the calculation of
Sagnac-like effects, the redshift formula (37) can be evaluated piecewise along broken lightlike
geodesics [23].
Angular diameter distances.
The notion of angular diameter distance is based on the intuitive idea that the farther an object is away the
smaller it looks, according to the rule
The formal definition needs the results of Section 2.3 on infinitesimally thin bundles. One considers a
past-oriented lightlike geodesic  parametrized by affine distance, i.e.,
parametrized by affine distance, i.e.,  and
and
 , and along
, and along  an infinitesimally thin bundle with vertex at the observer, i.e., at
an infinitesimally thin bundle with vertex at the observer, i.e., at  .
Then the shape parameters
.
Then the shape parameters  and
and  (recall Figure 3) satisfy the initial conditions
(recall Figure 3) satisfy the initial conditions
 and
and  . They have the following physical meaning. If the observer sees a
circular image of (small) angular diameter
. They have the following physical meaning. If the observer sees a
circular image of (small) angular diameter  on his or her sky, the (small but extended) light
source at affine distance
on his or her sky, the (small but extended) light
source at affine distance  actually has an elliptical cross-section with extremal diameters
actually has an elliptical cross-section with extremal diameters
 . It is therefore reasonable to call
. It is therefore reasonable to call  and
and  the extremal angular diameter distances.
Near the vertex,
the extremal angular diameter distances.
Near the vertex,  and
and  are monotonously increasing functions of the affine distance,
are monotonously increasing functions of the affine distance,
 . Farther away from the vertex, however, they may become decreasing,
so the functions
. Farther away from the vertex, however, they may become decreasing,
so the functions  and
and  need not be invertible. At a caustic point of
multiplicity one, one of the two functions
need not be invertible. At a caustic point of
multiplicity one, one of the two functions  and
and  changes sign; at a caustic point of
multiplicity two, both change sign (recall Section 2.3). The image of a light source at affine
distance
changes sign; at a caustic point of
multiplicity two, both change sign (recall Section 2.3). The image of a light source at affine
distance  is said to have even parity if
is said to have even parity if  and odd parity if
and odd parity if  .
Images with odd parity show the neighborhood of the light source side-inverted in comparison to
images with even parity. Clearly,
.
Images with odd parity show the neighborhood of the light source side-inverted in comparison to
images with even parity. Clearly,  and
and  are reasonable distance measures only in a
neighborhood of the vertex where they are monotonously increasing. However, the physical relevance
of
are reasonable distance measures only in a
neighborhood of the vertex where they are monotonously increasing. However, the physical relevance
of  and
and  lies in the fact that they relate cross-sectional diameters at the source to
angular diameters at the observer, and this is always true, even beyond caustic points.
lies in the fact that they relate cross-sectional diameters at the source to
angular diameters at the observer, and this is always true, even beyond caustic points.  and
and
 depend on the 4-velocity
depend on the 4-velocity  of the observer but not on the 4-velocity
of the observer but not on the 4-velocity  of the
source. This reflects the fact that the angular diameter of an image on the observer’s sky is
subject to aberration whereas the cross-sectional diameter of an infinitesimally thin bundle has
an invariant meaning (recall Section 2.3). Hence, if the observer’s worldline
of the
source. This reflects the fact that the angular diameter of an image on the observer’s sky is
subject to aberration whereas the cross-sectional diameter of an infinitesimally thin bundle has
an invariant meaning (recall Section 2.3). Hence, if the observer’s worldline  has been
specified,
has been
specified,  and
and  are well-defined functions of the observational coordinates
are well-defined functions of the observational coordinates  .
.
Area distance.
The area distance  is defined according to the idea
is defined according to the idea
As a formal definition for  , in terms of the extremal angular diameter distances
, in terms of the extremal angular diameter distances  and
and  as
functions of affine distance
as
functions of affine distance  , we use the equation
, we use the equation
 indeed relates, for a bundle with vertex at the observer, the cross-sectional area at the source to
the opening solid angle at the observer. Such a bundle has a caustic point exactly at those points where
indeed relates, for a bundle with vertex at the observer, the cross-sectional area at the source to
the opening solid angle at the observer. Such a bundle has a caustic point exactly at those points where
 . The area distance is often called “angular diameter distance” although, as indicated by
Equation (41), the name “averaged angular diameter distance” would be more appropriate. Just as
. The area distance is often called “angular diameter distance” although, as indicated by
Equation (41), the name “averaged angular diameter distance” would be more appropriate. Just as  and
and  , the area distance depends on the 4-velocity
, the area distance depends on the 4-velocity  of the observer but not on the 4-velocity
of the observer but not on the 4-velocity  of the light source. The area distance is observable for a light source whose true size is known (or can be
reasonably estimated). It is sometimes convenient to introduce the magnification or amplification factor
The absolute value of
of the light source. The area distance is observable for a light source whose true size is known (or can be
reasonably estimated). It is sometimes convenient to introduce the magnification or amplification factor
The absolute value of  determines the area distance, and the sign of
determines the area distance, and the sign of  determines the parity. In
Minkowski spacetime,
determines the parity. In
Minkowski spacetime,  and, thus,
and, thus,  . Hence,
. Hence,  means that a (small but
extended) light source at affine distance
means that a (small but
extended) light source at affine distance  subtends a larger solid angle on the observer’s sky than a light
source of the same size at the same affine distance in Minkowski spacetime. Note that in a multiple-imaging
situation the individual images may have different affine distances. Thus, the relative magnification factor
of two images is not directly observable. This is an important difference to the magnification
factor that is used in the quasi-Newtonian approximation formalism of lensing. The latter is
defined by comparison with an “unlensed image” (see, e.g., [298
subtends a larger solid angle on the observer’s sky than a light
source of the same size at the same affine distance in Minkowski spacetime. Note that in a multiple-imaging
situation the individual images may have different affine distances. Thus, the relative magnification factor
of two images is not directly observable. This is an important difference to the magnification
factor that is used in the quasi-Newtonian approximation formalism of lensing. The latter is
defined by comparison with an “unlensed image” (see, e.g., [298 ]), a notion that makes sense
only if the metric is viewed as a perturbation of some “background” metric. One can derive a
differential equation for the area distance (or, equivalently, for the magnification factor) as a function
of affine distance in the following way. On every parameter interval where
]), a notion that makes sense
only if the metric is viewed as a perturbation of some “background” metric. One can derive a
differential equation for the area distance (or, equivalently, for the magnification factor) as a function
of affine distance in the following way. On every parameter interval where  has no
zeros, the real part of Equation (27) shows that the area distance is related to the expansion by
Insertion into the Sachs equation (25) for
has no
zeros, the real part of Equation (27) shows that the area distance is related to the expansion by
Insertion into the Sachs equation (25) for  gives the focusing equation
Between the vertex at
gives the focusing equation
Between the vertex at  and the first conjugate point (caustic point),
and the first conjugate point (caustic point),  is determined by
Equation (44) and the initial conditions
The Ricci term in Equation (44) is non-negative if Einstein’s field equation holds and if the energy density
is non-negative for all observers (“weak energy condition”). Then Equations (44, 45) imply that
i.e.,
is determined by
Equation (44) and the initial conditions
The Ricci term in Equation (44) is non-negative if Einstein’s field equation holds and if the energy density
is non-negative for all observers (“weak energy condition”). Then Equations (44, 45) imply that
i.e.,  , for all
, for all  between the vertex at
between the vertex at  and the first conjugate point. In Minkowski
spacetime, Equation (46) holds with equality. Hence, Equation (46) says that the gravitational field has a
focusing, as opposed to a defocusing, effect. This is sometimes called the focusing theorem.
and the first conjugate point. In Minkowski
spacetime, Equation (46) holds with equality. Hence, Equation (46) says that the gravitational field has a
focusing, as opposed to a defocusing, effect. This is sometimes called the focusing theorem.
Corrected luminosity distance.
The idea of defining distance measures in terms of bundle cross-sections dates back to Tolman [322] and
Whittaker [351]. Originally, this idea was applied not to bundles with vertex at the observer but rather to
bundles with vertex at the light source. The resulting analogue of the area distance is the so-called
corrected luminosity distance  . It relates, for a bundle with vertex at the light source, the
cross-sectional area at the observer to the opening solid angle at the light source. Owing to
Etherington’s reciprocity law (35), area distance and corrected luminosity distance are related by
. It relates, for a bundle with vertex at the light source, the
cross-sectional area at the observer to the opening solid angle at the light source. Owing to
Etherington’s reciprocity law (35), area distance and corrected luminosity distance are related by
The redshift factor has its origin in the fact that the definition of  refers to an affine parametrization
adapted to
refers to an affine parametrization
adapted to  , and the definition of
, and the definition of  refers to an affine parametrization adapted to
refers to an affine parametrization adapted to  .
While
.
While  depends on
depends on  but not on
but not on  ,
,  depends on
depends on  but not on
but not on  .
.
Luminosity distance.
The physical meaning of the corrected luminosity distance is most easily understood in the
photon picture. For photons isotropically emitted from a light source, the percentage that hit a
prescribed area at the observer is proportional to  . As the energy of each photon
undergoes a redshift, the energy flux at the observer is proportional to
. As the energy of each photon
undergoes a redshift, the energy flux at the observer is proportional to  , where
, where
Thus, 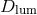 is the relevant quantity for calculating the luminosity (apparent brightness) of pointlike light
sources (see Equation (52)). For this reason
is the relevant quantity for calculating the luminosity (apparent brightness) of pointlike light
sources (see Equation (52)). For this reason  is called the (uncorrected) luminosity distance.
The observation that the purely geometric quantity
is called the (uncorrected) luminosity distance.
The observation that the purely geometric quantity  must be modified by an additional
redshift factor to give the energy flux is due to Walker [342].
must be modified by an additional
redshift factor to give the energy flux is due to Walker [342].  depends on the 4-velocity
depends on the 4-velocity
 of the observer and of the 4-velocity
of the observer and of the 4-velocity  of the light source.
of the light source.  and
and  can be
viewed as functions of the observational coordinates
can be
viewed as functions of the observational coordinates  if a vector field
if a vector field  with
with
 has been distinguished, one integral curve of
has been distinguished, one integral curve of  is chosen as the observer, and the other
integral curves of
is chosen as the observer, and the other
integral curves of  are chosen as the light sources. In that case Equation (38) implies that not
only
are chosen as the light sources. In that case Equation (38) implies that not
only  but also
but also  and
and  are of the form
are of the form  . Thus, near the
observer all three distance measures coincide with Euclidean distance in the observer’s rest space.
. Thus, near the
observer all three distance measures coincide with Euclidean distance in the observer’s rest space.
Parallax distance.
In an arbitrary spacetime, we fix an observation event  and the observer’s 4-velocity
and the observer’s 4-velocity  . We consider
a past-oriented lightlike geodesic
. We consider
a past-oriented lightlike geodesic  parametrized by affine distance,
parametrized by affine distance,  and
and  .
To a light source passing through the event
.
To a light source passing through the event  we assign the (averaged) parallax distance
we assign the (averaged) parallax distance
 , where
, where  is the expansion of an infinitesimally thin bundle with vertex
at
is the expansion of an infinitesimally thin bundle with vertex
at  . This definition follows [171]. Its relevance in view of cosmology was discussed in
detail by Rosquist [288
. This definition follows [171]. Its relevance in view of cosmology was discussed in
detail by Rosquist [288 ].
].  can be measured by performing the standard trigonometric
parallax method of elementary Euclidean geometry, with the observer at
can be measured by performing the standard trigonometric
parallax method of elementary Euclidean geometry, with the observer at  and an assistant
observer at the perimeter of the bundle, and then averaging over all possible positions of the
assistant. Note that the method refers to a bundle with vertex at the light source, i.e., to light
rays that leave the light source simultaneously. (Averaging is not necessary if this bundle is
circular.)
and an assistant
observer at the perimeter of the bundle, and then averaging over all possible positions of the
assistant. Note that the method refers to a bundle with vertex at the light source, i.e., to light
rays that leave the light source simultaneously. (Averaging is not necessary if this bundle is
circular.)  depends on the 4-velocity of the observer but not on the 4-velocity of the light
source. To within first-order approximation near the observer it coincides with affine distance
(recall Equation (32)). For the potential obervational relevance of
depends on the 4-velocity of the observer but not on the 4-velocity of the light
source. To within first-order approximation near the observer it coincides with affine distance
(recall Equation (32)). For the potential obervational relevance of  see [288], and [298
see [288], and [298 ],
p. 509.
],
p. 509.
In view of lensing,  ,
,  , and
, and  are the most important distance measures because they are
related to image distortion (see Section 2.5) and to the brightness of images (see Section 2.6). In
spacetimes with many symmetries, these quantities can be explicitly calculated (see Section 4.1
for conformally flat spactimes, and Section 4.3 for spherically symmetric static spacetimes).
This is impossible in a spacetime without symmetries, in particular in a realistic cosmological
model with inhomogeneities (“clumpy universe”). Following Kristian and Sachs [189
are the most important distance measures because they are
related to image distortion (see Section 2.5) and to the brightness of images (see Section 2.6). In
spacetimes with many symmetries, these quantities can be explicitly calculated (see Section 4.1
for conformally flat spactimes, and Section 4.3 for spherically symmetric static spacetimes).
This is impossible in a spacetime without symmetries, in particular in a realistic cosmological
model with inhomogeneities (“clumpy universe”). Following Kristian and Sachs [189 ], one often
uses series expansions with respect to
], one often
uses series expansions with respect to  . For statistical considerations one may work with
the focusing equation in a Friedmann–Robertson–Walker spacetime with average density (see
Section 4.1), or with a heuristically modified focusing equation taking clumps into account.
The latter leads to the so-called Dyer–Roeder distance [86, 87] which is discussed in several
text-books (see, e.g., [298
. For statistical considerations one may work with
the focusing equation in a Friedmann–Robertson–Walker spacetime with average density (see
Section 4.1), or with a heuristically modified focusing equation taking clumps into account.
The latter leads to the so-called Dyer–Roeder distance [86, 87] which is discussed in several
text-books (see, e.g., [298 ]). (For pre-Dyer–Roeder papers on optics in cosmological models
with inhomogeneities, see the historical notes in [173].) As overdensities have a focusing and
underdensities have a defocusing effect, it is widely believed (following [344]) that after averaging
over sufficiently large angular scales the Friedmann–Robertson–Walker calculation gives the
correct distance-redshift relation. However, it was argued by Ellis, Bassett, and Dunsby [99]
that caustics produced by the lensing effect of overdensities lead to a systematic bias towards
smaller angular sizes (“shrinking”). For a spherically symmetric inhomogeneity, the effect on
the distance-redshift relation can be calculated analytically [231]. For thorough discussions
of light propagation in a clumpy universe also see Pyne and Birkinshaw [284], and Holz and
Wald [160].
]). (For pre-Dyer–Roeder papers on optics in cosmological models
with inhomogeneities, see the historical notes in [173].) As overdensities have a focusing and
underdensities have a defocusing effect, it is widely believed (following [344]) that after averaging
over sufficiently large angular scales the Friedmann–Robertson–Walker calculation gives the
correct distance-redshift relation. However, it was argued by Ellis, Bassett, and Dunsby [99]
that caustics produced by the lensing effect of overdensities lead to a systematic bias towards
smaller angular sizes (“shrinking”). For a spherically symmetric inhomogeneity, the effect on
the distance-redshift relation can be calculated analytically [231]. For thorough discussions
of light propagation in a clumpy universe also see Pyne and Birkinshaw [284], and Holz and
Wald [160].
![]() for each lightlike geodesic through the observation
event
for each lightlike geodesic through the observation
event ![]() such that
such that ![]() and
and ![]() . Then the affine parameter
. Then the affine parameter ![]() itself
can be viewed as a distance measure. This affine distance has the desirable features that it
increases monotonously along each ray and that it coincides in an infinitesimal neighborhood
of
itself
can be viewed as a distance measure. This affine distance has the desirable features that it
increases monotonously along each ray and that it coincides in an infinitesimal neighborhood
of ![]() with Euclidean distance in the rest system of
with Euclidean distance in the rest system of ![]() . The affine distance depends on
the 4-velocity
. The affine distance depends on
the 4-velocity ![]() of the observer but not on the 4-velocity
of the observer but not on the 4-velocity ![]() of the light source. It is a
mathematically very convenient notion, but it is not an observable. (It can be operationally realized in
terms of an observer field whose 4-velocities are parallel along the ray. Then the affine distance
results by integration if each observer measures the length of an infinitesimally short part of the
ray in his rest system. However, in view of astronomical situations this is a purely theoretical
construction.) The notion of affine distance was introduced by Kermack, McCrea, and Whittaker [179
of the light source. It is a
mathematically very convenient notion, but it is not an observable. (It can be operationally realized in
terms of an observer field whose 4-velocities are parallel along the ray. Then the affine distance
results by integration if each observer measures the length of an infinitesimally short part of the
ray in his rest system. However, in view of astronomical situations this is a purely theoretical
construction.) The notion of affine distance was introduced by Kermack, McCrea, and Whittaker [179![]() ].
].
![]() that slices the spacetime into spacelike hypersurfaces
that slices the spacetime into spacelike hypersurfaces ![]() . (Such a time
function globally exists if and only if the spacetime is stably causal; see, e.g., [153
. (Such a time
function globally exists if and only if the spacetime is stably causal; see, e.g., [153![]() ], p. 198.) The travel time
is equal to
], p. 198.) The travel time
is equal to ![]() , for each
, for each ![]() on the past light cone of
on the past light cone of ![]() . In other words, the intersection of
the light cone with a hypersurface
. In other words, the intersection of
the light cone with a hypersurface ![]() determines events of equal travel time; we call these
intersections “instantaneous wave fronts” (recall Section 2.2). Examples of instantaneous wave fronts are
shown in Figures 13
determines events of equal travel time; we call these
intersections “instantaneous wave fronts” (recall Section 2.2). Examples of instantaneous wave fronts are
shown in Figures 13![]() , 18
, 18![]() , 19
, 19![]() , 27
, 27![]() , and 28
, and 28![]() . The travel time increases monotonously along each ray. Clearly, it
depends neither on the 4-velocity
. The travel time increases monotonously along each ray. Clearly, it
depends neither on the 4-velocity ![]() of the observer nor on the 4-velocity
of the observer nor on the 4-velocity ![]() of the light
source. Note that the travel time has a unique value at each point of
of the light
source. Note that the travel time has a unique value at each point of ![]() ’s past light cone,
even at events that can be reached by two different rays from
’s past light cone,
even at events that can be reached by two different rays from ![]() . Near
. Near ![]() the travel time
coincides with Euclidean distance in the observer’s rest system only if
the travel time
coincides with Euclidean distance in the observer’s rest system only if ![]() is perpendicular to
the hypersurface
is perpendicular to
the hypersurface ![]() with
with ![]() . (The latter equation is true if along the
observer’s world line the time function
. (The latter equation is true if along the
observer’s world line the time function ![]() coincides with proper time.) The travel time is not
directly observable. However, travel time differences are observable in multiple-imaging situations
if the intrinsic luminosity of the light source is time-dependent. To illustrate this, think of a
light source that flashes at a particular instant. If the flash reaches the observer’s wordline
along two different rays, the proper time difference
coincides with proper time.) The travel time is not
directly observable. However, travel time differences are observable in multiple-imaging situations
if the intrinsic luminosity of the light source is time-dependent. To illustrate this, think of a
light source that flashes at a particular instant. If the flash reaches the observer’s wordline
along two different rays, the proper time difference ![]() of the two arrival events is directly
measurable. For a time function
of the two arrival events is directly
measurable. For a time function ![]() that along the observer’s worldline coincides with proper time,
this observed time delay
that along the observer’s worldline coincides with proper time,
this observed time delay ![]() gives the difference in travel time for the two rays. In view of
applications, the measurement of time delays is of great relevance for quasar lensing. For the double
quasar 0957+561 the observed time delay
gives the difference in travel time for the two rays. In view of
applications, the measurement of time delays is of great relevance for quasar lensing. For the double
quasar 0957+561 the observed time delay ![]() is about 417 days (see, e.g., [275
is about 417 days (see, e.g., [275![]() ], p. 149).
], p. 149).
![]() that connects the observation event
that connects the observation event ![]() on the worldline
on the worldline ![]() of the observer with the emission event
of the observer with the emission event ![]() on the worldline
on the worldline ![]() of the light source, one
considers a neighboring lightlike geodesic that meets
of the light source, one
considers a neighboring lightlike geodesic that meets ![]() at a proper time interval
at a proper time interval ![]() from
from ![]() and
and ![]() at a proper time interval
at a proper time interval ![]() from
from ![]() . The redshift
. The redshift ![]() is defined as
is defined as
![]() is defined according to the idea
is defined according to the idea ![]() . It relates, for a bundle with vertex at the light source, the
cross-sectional area at the observer to the opening solid angle at the light source. Owing to
Etherington’s reciprocity law (35
. It relates, for a bundle with vertex at the light source, the
cross-sectional area at the observer to the opening solid angle at the light source. Owing to
Etherington’s reciprocity law (35![]() ), area distance and corrected luminosity distance are related by
), area distance and corrected luminosity distance are related by
![]() . As the energy of each photon
undergoes a redshift, the energy flux at the observer is proportional to
. As the energy of each photon
undergoes a redshift, the energy flux at the observer is proportional to ![]() , where
, where
![]() and the observer’s 4-velocity
and the observer’s 4-velocity ![]() . We consider
a past-oriented lightlike geodesic
. We consider
a past-oriented lightlike geodesic ![]() parametrized by affine distance,
parametrized by affine distance, ![]() and
and ![]() .
To a light source passing through the event
.
To a light source passing through the event ![]() we assign the (averaged) parallax distance
we assign the (averaged) parallax distance
![]() , where
, where ![]() is the expansion of an infinitesimally thin bundle with vertex
at
is the expansion of an infinitesimally thin bundle with vertex
at ![]() . This definition follows [171]. Its relevance in view of cosmology was discussed in
detail by Rosquist [288
. This definition follows [171]. Its relevance in view of cosmology was discussed in
detail by Rosquist [288![]() ].
]. ![]() can be measured by performing the standard trigonometric
parallax method of elementary Euclidean geometry, with the observer at
can be measured by performing the standard trigonometric
parallax method of elementary Euclidean geometry, with the observer at ![]() and an assistant
observer at the perimeter of the bundle, and then averaging over all possible positions of the
assistant. Note that the method refers to a bundle with vertex at the light source, i.e., to light
rays that leave the light source simultaneously. (Averaging is not necessary if this bundle is
circular.)
and an assistant
observer at the perimeter of the bundle, and then averaging over all possible positions of the
assistant. Note that the method refers to a bundle with vertex at the light source, i.e., to light
rays that leave the light source simultaneously. (Averaging is not necessary if this bundle is
circular.) ![]() depends on the 4-velocity of the observer but not on the 4-velocity of the light
source. To within first-order approximation near the observer it coincides with affine distance
(recall Equation (32
depends on the 4-velocity of the observer but not on the 4-velocity of the light
source. To within first-order approximation near the observer it coincides with affine distance
(recall Equation (32![]() )). For the potential obervational relevance of
)). For the potential obervational relevance of ![]() see [288], and [298
see [288], and [298![]() ],
p. 509.
],
p. 509.
![]() ,
, ![]() , and
, and ![]() are the most important distance measures because they are
related to image distortion (see Section 2.5) and to the brightness of images (see Section 2.6). In
spacetimes with many symmetries, these quantities can be explicitly calculated (see Section 4.1
for conformally flat spactimes, and Section 4.3 for spherically symmetric static spacetimes).
This is impossible in a spacetime without symmetries, in particular in a realistic cosmological
model with inhomogeneities (“clumpy universe”). Following Kristian and Sachs [189
are the most important distance measures because they are
related to image distortion (see Section 2.5) and to the brightness of images (see Section 2.6). In
spacetimes with many symmetries, these quantities can be explicitly calculated (see Section 4.1
for conformally flat spactimes, and Section 4.3 for spherically symmetric static spacetimes).
This is impossible in a spacetime without symmetries, in particular in a realistic cosmological
model with inhomogeneities (“clumpy universe”). Following Kristian and Sachs [189![]() ], one often
uses series expansions with respect to
], one often
uses series expansions with respect to ![]() . For statistical considerations one may work with
the focusing equation in a Friedmann–Robertson–Walker spacetime with average density (see
Section 4.1), or with a heuristically modified focusing equation taking clumps into account.
The latter leads to the so-called Dyer–Roeder distance [86, 87] which is discussed in several
text-books (see, e.g., [298
. For statistical considerations one may work with
the focusing equation in a Friedmann–Robertson–Walker spacetime with average density (see
Section 4.1), or with a heuristically modified focusing equation taking clumps into account.
The latter leads to the so-called Dyer–Roeder distance [86, 87] which is discussed in several
text-books (see, e.g., [298![]() ]). (For pre-Dyer–Roeder papers on optics in cosmological models
with inhomogeneities, see the historical notes in [173].) As overdensities have a focusing and
underdensities have a defocusing effect, it is widely believed (following [344]) that after averaging
over sufficiently large angular scales the Friedmann–Robertson–Walker calculation gives the
correct distance-redshift relation. However, it was argued by Ellis, Bassett, and Dunsby [99]
that caustics produced by the lensing effect of overdensities lead to a systematic bias towards
smaller angular sizes (“shrinking”). For a spherically symmetric inhomogeneity, the effect on
the distance-redshift relation can be calculated analytically [231]. For thorough discussions
of light propagation in a clumpy universe also see Pyne and Birkinshaw [284], and Holz and
Wald [160].
]). (For pre-Dyer–Roeder papers on optics in cosmological models
with inhomogeneities, see the historical notes in [173].) As overdensities have a focusing and
underdensities have a defocusing effect, it is widely believed (following [344]) that after averaging
over sufficiently large angular scales the Friedmann–Robertson–Walker calculation gives the
correct distance-redshift relation. However, it was argued by Ellis, Bassett, and Dunsby [99]
that caustics produced by the lensing effect of overdensities lead to a systematic bias towards
smaller angular sizes (“shrinking”). For a spherically symmetric inhomogeneity, the effect on
the distance-redshift relation can be calculated analytically [231]. For thorough discussions
of light propagation in a clumpy universe also see Pyne and Birkinshaw [284], and Holz and
Wald [160].