4.3 Lensing in spherically symmetric and static spacetimes
The class of spherically symmetric and static spacetimes is of particular relevance in view of lensing,
because it includes models for non-rotating stars and black holes (see Sections 5.1, 5.2, 5.3), but also for
more exotic objects such as wormholes (see Section 5.4), monopoles (see Section 5.5), naked singularities
(see Section 5.6), and Boson or Fermion stars (see Section 5.7). Here we collect the relevant formulas for an
unspecified spherically symmetric and static metric. We find it convenient to write the metric in the form
As Equation (69) is a special case of Equation (61), all results of Section 4.2 for conformally stationary
metrics apply. However, much stronger results are possible because for metrics of the form (69) the geodesic
equation is completely integrable. Hence, all relevant quantities can be determined explicitly in terms of
integrals over the metric coefficients.
Redshift and Fermat geometry.
Comparison of Equation (69) with the general form (61) of a conformally stationary spacetime shows that
here the redshift potential  is a function of
is a function of  only, the Fermat one-form
only, the Fermat one-form  vanishes, and the Fermat
metric
vanishes, and the Fermat
metric  is of the special form
is of the special form
By Fermat’s principle, the geodesics of  coincide with the projection to 3-space of light rays.
The travel time (in terms of the time coordinate
coincide with the projection to 3-space of light rays.
The travel time (in terms of the time coordinate  ) of a lightlike curve coincides with the
) of a lightlike curve coincides with the
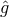 -arclength of its projection. By symmetry, every
-arclength of its projection. By symmetry, every  -geodesic stays in a plane through the
origin. From Equation (70) we read that the sphere of radius
-geodesic stays in a plane through the
origin. From Equation (70) we read that the sphere of radius  has area
has area  with
respect to the Fermat metric. Also, Equation (70) implies that the second fundamental form of
this sphere is a multiple of its first fundamental form, with a factor
with
respect to the Fermat metric. Also, Equation (70) implies that the second fundamental form of
this sphere is a multiple of its first fundamental form, with a factor  . If
the sphere
. If
the sphere  is totally geodesic, i.e., a
is totally geodesic, i.e., a  -geodesic that starts tangent to this sphere remains in it.
The best known example for such a light sphere or photon sphere is the sphere
-geodesic that starts tangent to this sphere remains in it.
The best known example for such a light sphere or photon sphere is the sphere  in the
Schwarzschild spacetime (see Section 5.1). Light spheres also occur in the spacetimes of wormholes (see
Section 5.4). If
in the
Schwarzschild spacetime (see Section 5.1). Light spheres also occur in the spacetimes of wormholes (see
Section 5.4). If  , the circular light rays in a light sphere are stable with respect to radial
perturbations, and if
, the circular light rays in a light sphere are stable with respect to radial
perturbations, and if  , they are unstable like in the Schwarschild case. The condition
under which a spherically symmetric static spacetime admits a light sphere was first given
by Atkinson [13
, they are unstable like in the Schwarschild case. The condition
under which a spherically symmetric static spacetime admits a light sphere was first given
by Atkinson [13 ]. Abramowicz [1] has shown that for an observer traveling along a circular
light orbit (with subluminal velocity) there is no centrifugal force and no gyroscopic precession.
Claudel, Virbhadra, and Ellis [59
]. Abramowicz [1] has shown that for an observer traveling along a circular
light orbit (with subluminal velocity) there is no centrifugal force and no gyroscopic precession.
Claudel, Virbhadra, and Ellis [59 ] investigated, with the help of Einstein’s field equation and
energy conditions, the amount of matter surrounded by a light sphere. Among other things,
they found an energy condition under which a spherically symmetric static black hole must
be surrounded by a light sphere. A purely kinematical argument shows that any spherically
symmetric and static spacetime that has a horizon at
] investigated, with the help of Einstein’s field equation and
energy conditions, the amount of matter surrounded by a light sphere. Among other things,
they found an energy condition under which a spherically symmetric static black hole must
be surrounded by a light sphere. A purely kinematical argument shows that any spherically
symmetric and static spacetime that has a horizon at  and is asymptotically flat for
and is asymptotically flat for
 must contain a light sphere at some radius between
must contain a light sphere at some radius between  and
and  (see Hasse and
Perlick [152
(see Hasse and
Perlick [152 ]). In the same article, it is shown that in any spherically symmetric static spacetime with a
light sphere there is gravitational lensing with infinitely many images. Bozza [37
]). In the same article, it is shown that in any spherically symmetric static spacetime with a
light sphere there is gravitational lensing with infinitely many images. Bozza [37 ] investigated
a strong-field limit of lensing in spherically symmetric static spacetimes, as opposed to the
well-known weak-field limit, which applies to light rays that come close to an unstable light
sphere. (Actually, the term “strong-bending limit” would be more appropriate because the
gravitational field, measured in terms of tidal forces, need not be particularly strong near an
unstable light sphere.) This limit applies, in particular, to light rays that approach the sphere
] investigated
a strong-field limit of lensing in spherically symmetric static spacetimes, as opposed to the
well-known weak-field limit, which applies to light rays that come close to an unstable light
sphere. (Actually, the term “strong-bending limit” would be more appropriate because the
gravitational field, measured in terms of tidal forces, need not be particularly strong near an
unstable light sphere.) This limit applies, in particular, to light rays that approach the sphere
 in the Schwarzschild spacetime (see [39
in the Schwarzschild spacetime (see [39 ] and, for illustrations, Figures 15, 16, and 17).
] and, for illustrations, Figures 15, 16, and 17).
Index of refraction and embedding diagrams.
Transformation to an isotropic radius coordinate  via
via
takes the Fermat metric (70) to the form
where
On the right-hand side  has to be expressed by
has to be expressed by  with the help of Equation (72). The results of
Section 4.2 imply that the lightlike geodesics in a spherically symmetric static spacetime are equivalent to
the light rays in a medium with index of refraction (74) on Euclidean 3-space. For arbitrary metrics of the
form (69), this result is due to Atkinson [13
with the help of Equation (72). The results of
Section 4.2 imply that the lightlike geodesics in a spherically symmetric static spacetime are equivalent to
the light rays in a medium with index of refraction (74) on Euclidean 3-space. For arbitrary metrics of the
form (69), this result is due to Atkinson [13 ]. It reduces the lightlike geodesic problem in a spherically
symmetric static spacetime to a standard problem in ordinary optics, as treated, e.g., in [213], §27,
and [198], Section 4. One can combine this result with our earlier observation that the integral in
Equation (67) has the same form as the functional in Maupertuis’ principle in classical mechanics. This
demonstrates that light rays in spherically symmetric and static spacetimes behave like particles in a
spherically symmetric potential on Euclidean 3-space (cf., e.g., [104
]. It reduces the lightlike geodesic problem in a spherically
symmetric static spacetime to a standard problem in ordinary optics, as treated, e.g., in [213], §27,
and [198], Section 4. One can combine this result with our earlier observation that the integral in
Equation (67) has the same form as the functional in Maupertuis’ principle in classical mechanics. This
demonstrates that light rays in spherically symmetric and static spacetimes behave like particles in a
spherically symmetric potential on Euclidean 3-space (cf., e.g., [104 ]). If the embeddability condition
is satisfied, we define a function
]). If the embeddability condition
is satisfied, we define a function  by
Then the Fermat metric (70) reads
If restricted to the equatorial plane
by
Then the Fermat metric (70) reads
If restricted to the equatorial plane  , the metric (77) describes a surface of revolution, embedded
into Euclidean 3-space as
Such embeddings of the Fermat geometry have been visualized for several spacetimes of interest (see
Figure 11 for the Schwarzschild case and [159
, the metric (77) describes a surface of revolution, embedded
into Euclidean 3-space as
Such embeddings of the Fermat geometry have been visualized for several spacetimes of interest (see
Figure 11 for the Schwarzschild case and [159 ] for other examples). This is quite instructive because from a
picture of a surface of revolution one can read the qualitative features of its geodesics without calculating
them. Note that Equation (72) defines the isotropic radius coordinate uniquely up to a multiplicative
constant. Hence, the straight lines in this coordinate representation give us an unambiguously defined
reference grid for every spherically symmetric and static spacetime. These straight lines have been called
triangulation lines in [62, 63], where their use for calculating bending angles, exactly or approximately, is
outlined.
] for other examples). This is quite instructive because from a
picture of a surface of revolution one can read the qualitative features of its geodesics without calculating
them. Note that Equation (72) defines the isotropic radius coordinate uniquely up to a multiplicative
constant. Hence, the straight lines in this coordinate representation give us an unambiguously defined
reference grid for every spherically symmetric and static spacetime. These straight lines have been called
triangulation lines in [62, 63], where their use for calculating bending angles, exactly or approximately, is
outlined.
Light cone.
In a spherically symmetric static spacetime, the (past) light cone of an event  can be written in terms
of integrals over the metric coefficients. We first restrict to the equatorial plane
can be written in terms
of integrals over the metric coefficients. We first restrict to the equatorial plane  . The
. The
 -geodesics are then determined by the Lagrangian
-geodesics are then determined by the Lagrangian
For fixed radius value  , initial conditions
determine a unique solution
, initial conditions
determine a unique solution  ,
,  of the Euler–Lagrange equations.
of the Euler–Lagrange equations.  measures
the initial direction with respect to the symmetry axis (see Figure 6). We get all light rays issuing from the
event
measures
the initial direction with respect to the symmetry axis (see Figure 6). We get all light rays issuing from the
event  ,
,  ,
,  ,
,  into the past by letting
into the past by letting  range from 0 to
range from 0 to  and
applying rotations around the symmetry axis. This gives us the past light cone of this event in the form
and
applying rotations around the symmetry axis. This gives us the past light cone of this event in the form
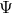 and
and  are spherical coordinates on the observer’s sky. If we let
are spherical coordinates on the observer’s sky. If we let  float over
float over  , we
get the observational coordinates (4) for an observer on a
, we
get the observational coordinates (4) for an observer on a  -line, up to two modifications.
First,
-line, up to two modifications.
First, 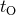 is not the same as proper time
is not the same as proper time  ; however, they are related just by a constant,
Second,
; however, they are related just by a constant,
Second,  is not the same as the affine parameter
is not the same as the affine parameter  ; along a ray with initial direction
; along a ray with initial direction  , they are
related by
The constants of motion
give us the functions
, they are
related by
The constants of motion
give us the functions  ,
,  in terms of integrals,
Here the notation with the dots is a short-hand; it means that the integral is to be decomposed into sections
where
in terms of integrals,
Here the notation with the dots is a short-hand; it means that the integral is to be decomposed into sections
where  is a monotonous function of
is a monotonous function of  , and that the absolute value of the integrals over all
sections have to be added up. Turning points occur at radius values where
, and that the absolute value of the integrals over all
sections have to be added up. Turning points occur at radius values where  and
and
 (see Figure 9). If the metric coefficients
(see Figure 9). If the metric coefficients  and
and  have been specified, these integrals can
be calculated and give us the light cone (see Figure 12 for an example). Having parametrized the
rays with
have been specified, these integrals can
be calculated and give us the light cone (see Figure 12 for an example). Having parametrized the
rays with  -arclength (= travel time), we immediately get the intersections of the light cone
with hypersurfaces
-arclength (= travel time), we immediately get the intersections of the light cone
with hypersurfaces  (“instantaneous wave fronts”); see Figures 13, 18, and 19.
(“instantaneous wave fronts”); see Figures 13, 18, and 19.
Exact lens map.
Recall from Section 2.1 that the exact lens map [122 ] refers to a chosen observation event
] refers to a chosen observation event  and a
chosen “source surface”
and a
chosen “source surface”  . In general, for
. In general, for  we may choose any 3-dimensional submanifold that is
ruled by timelike curves. The latter are to be interpreted as wordlines of light sources. In a spherically
symmetric and static spacetime, we may take advantage of the symmetry by choosing for
we may choose any 3-dimensional submanifold that is
ruled by timelike curves. The latter are to be interpreted as wordlines of light sources. In a spherically
symmetric and static spacetime, we may take advantage of the symmetry by choosing for  a
sphere
a
sphere  with its ruling by the
with its ruling by the 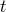 -lines. This restricts the consideration to lensing for
static light sources. Note that all static light sources at radius
-lines. This restricts the consideration to lensing for
static light sources. Note that all static light sources at radius  undergo the same redshift,
undergo the same redshift,
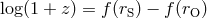 . Without loss of generality, we place the observation event
. Without loss of generality, we place the observation event  on the 3-axis
at radius
on the 3-axis
at radius  . This gives us the past light cone in the representation (81). To each ray from the
observer, with initial direction characterized by
. This gives us the past light cone in the representation (81). To each ray from the
observer, with initial direction characterized by  , we can assign the total angle
, we can assign the total angle  the ray
sweeps out on its way from
the ray
sweeps out on its way from  to
to  (see Figure 6).
(see Figure 6).  is given by Equation (86),
is given by Equation (86),
where the same short-hand notation is used as in Equation (86).  is not necessarily defined for all
is not necessarily defined for all
 because not all light rays that start at
because not all light rays that start at  may reach
may reach 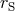 . Also,
. Also,  may be multi-valued
because a light ray may intersect the sphere
may be multi-valued
because a light ray may intersect the sphere  several times. Equation (81) gives us the (possibly
multi-valued) lens map
It assigns to each point on the observer’s sky the position of the light source which is seen at that point.
several times. Equation (81) gives us the (possibly
multi-valued) lens map
It assigns to each point on the observer’s sky the position of the light source which is seen at that point.
 may take all values between 0 and infinity. For each image we can define the order
which counts how often the ray has met the axis. The standard example where images of arbitrarily high
order occur is the Schwarzschild spacetime (see Section 5.1). For many, though not all, applications one
may restrict to the case that the spacetime is asymptotically flat and that
may take all values between 0 and infinity. For each image we can define the order
which counts how often the ray has met the axis. The standard example where images of arbitrarily high
order occur is the Schwarzschild spacetime (see Section 5.1). For many, though not all, applications one
may restrict to the case that the spacetime is asymptotically flat and that  and
and 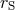 are so large that
the spacetime is almost flat at these radius values. For a light ray with turning point at
are so large that
the spacetime is almost flat at these radius values. For a light ray with turning point at 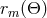 ,
Equation (87) can then be approximated by
If the entire ray remains in the region where the spacetime is almost flat, Equation (90) gives the usual
weak-field approximation of light bending with
,
Equation (87) can then be approximated by
If the entire ray remains in the region where the spacetime is almost flat, Equation (90) gives the usual
weak-field approximation of light bending with  close to
close to 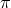 . However, Equation (90) does not
require that the ray stays in the region that is almost flat. The integral in Equation (90) becomes
arbitrarily large if
. However, Equation (90) does not
require that the ray stays in the region that is almost flat. The integral in Equation (90) becomes
arbitrarily large if 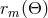 comes close to an unstable light sphere,
comes close to an unstable light sphere,  and
and  . This
situation is well known to occur in the Schwarzschild spacetime with
. This
situation is well known to occur in the Schwarzschild spacetime with  (see Section 5.1, in
particular Figures 9, 14, and 15). The divergence of
(see Section 5.1, in
particular Figures 9, 14, and 15). The divergence of  is always logarithmic [37
is always logarithmic [37 ]. Virbhadra and
Ellis [336
]. Virbhadra and
Ellis [336 ] (cf. [338
] (cf. [338 ] for an earlier version) approximately evaluate Equation (90) for the case that source
and observer are almost aligned, i.e., that
] for an earlier version) approximately evaluate Equation (90) for the case that source
and observer are almost aligned, i.e., that  is close to an odd multiple of
is close to an odd multiple of  . This corresponds to
replacing the sphere at
. This corresponds to
replacing the sphere at  with its tangent plane. The resulting “almost exact lens map” takes an
intermediary position between the exact treatment and the quasi-Newtonian approximation. It was
originally introduced for the Schwarzschild metric [336
with its tangent plane. The resulting “almost exact lens map” takes an
intermediary position between the exact treatment and the quasi-Newtonian approximation. It was
originally introduced for the Schwarzschild metric [336 ] where it approximates the exact treatment
remarkably well within a wide range of validity [118
] where it approximates the exact treatment
remarkably well within a wide range of validity [118 ]. On the other hand, neither analytical nor numerical
evaluation of the “almost exact lens map” is significantly easier than that of the exact lens map.
For situations where the assumption of almost perfect alignment cannot be maintained the
Virbhadra–Ellis lens equation must be modified (see [70
]. On the other hand, neither analytical nor numerical
evaluation of the “almost exact lens map” is significantly easier than that of the exact lens map.
For situations where the assumption of almost perfect alignment cannot be maintained the
Virbhadra–Ellis lens equation must be modified (see [70 ]; related material can also be found
in [38
]; related material can also be found
in [38 ]).
]).
4.3.0.1 Distance measures, image distortion and brightness of images.
For calculating image distortion (see Section 2.5) and the brightness of images (see Section 2.6) we have to
consider infinitesimally thin bundles with vertex at the observer. In a spherically symmetric and
static spacetime, we can apply the orthonormal derivative operators  and
and  to the
representation (81) of the past light cone. Along each ray, this gives us two Jacobi fields
to the
representation (81) of the past light cone. Along each ray, this gives us two Jacobi fields  and
and  which span an infinitesimally thin bundle with vertex at the observer.
which span an infinitesimally thin bundle with vertex at the observer.  points in the radial direction
and
points in the radial direction
and 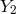 points in the tangential direction (see Figure 7). The radial and the tangential direction
are orthogonal to each other and, by symmetry, parallel-transported along each ray. Thus,
in contrast to the general situation of Figure 3,
points in the tangential direction (see Figure 7). The radial and the tangential direction
are orthogonal to each other and, by symmetry, parallel-transported along each ray. Thus,
in contrast to the general situation of Figure 3,  and
and  are related to a Sachs basis
are related to a Sachs basis
 simply by
simply by  and
and  . The coefficients
. The coefficients  and
and  are the
extremal angular diameter distances of Section 2.4 with respect to a static observer (because the
are the
extremal angular diameter distances of Section 2.4 with respect to a static observer (because the
 -grid refers to a static observer). In the case at hand, they are called the radial and
tangential angular diameter distances. They can be calculated by normalizing
-grid refers to a static observer). In the case at hand, they are called the radial and
tangential angular diameter distances. They can be calculated by normalizing  and
and  ,
These formulas have been derived first for the special case of the Schwarzschild metric by Dwivedi and
Kantowski [84
,
These formulas have been derived first for the special case of the Schwarzschild metric by Dwivedi and
Kantowski [84 ] and then for arbitrary spherically symmetric static spacetimes by Dyer [85
] and then for arbitrary spherically symmetric static spacetimes by Dyer [85 ]. (In [85
]. (In [85 ],
Equation (92) is erroneously given only for the case that, in our notation,
],
Equation (92) is erroneously given only for the case that, in our notation, 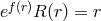 .) From these
formulas we immediately get the area distance
.) From these
formulas we immediately get the area distance  for a static observer and, with the help
of the redshift
for a static observer and, with the help
of the redshift  , the luminosity distance
, the luminosity distance  (recall Section 2.4). In this way,
Equation (91) and Equation (92) allow to calculate the brightness of images according to the formulas of
Section 2.6. Similarly, Equation (91) and Equation (92) allow to calculate image distortion in terms of the
ellipticity
(recall Section 2.4). In this way,
Equation (91) and Equation (92) allow to calculate the brightness of images according to the formulas of
Section 2.6. Similarly, Equation (91) and Equation (92) allow to calculate image distortion in terms of the
ellipticity  (recall Section 2.5). In general,
(recall Section 2.5). In general,  is a complex quantity, defined by Equation (49). In the
case at hand, it reduces to the real quantity
is a complex quantity, defined by Equation (49). In the
case at hand, it reduces to the real quantity  . The expansion
. The expansion 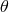 and the shear
and the shear
 of the bundles under consideration can be calculated from Kantowski’s formula [172, 84
of the bundles under consideration can be calculated from Kantowski’s formula [172, 84 ],
to which Equation (27) reduces in the case at hand. The dot (= derivative with respect to the affine
parameter
],
to which Equation (27) reduces in the case at hand. The dot (= derivative with respect to the affine
parameter  ) is related to the derivative with respect to
) is related to the derivative with respect to 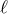 by Equation (83). Evaluating Equations (91,
92) in connection with the exact lens map leads to quite convenient formulas, for static light sources at
by Equation (83). Evaluating Equations (91,
92) in connection with the exact lens map leads to quite convenient formulas, for static light sources at
 . Setting
. Setting  and
and  and comparing with Equation (87) yields (cf. [271
and comparing with Equation (87) yields (cf. [271 ])
These formulas immediately give image distortion and the brightness of images if the map
])
These formulas immediately give image distortion and the brightness of images if the map 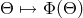 is
known.
is
known.
Caustics of light cones.
Quite generally, the past light cone has a caustic point exactly where at least one of the extremal angular
diameter distances  ,
,  vanishes (see Sections 2.2, 2.3, and 2.4). In the case at hand, zeros of
vanishes (see Sections 2.2, 2.3, and 2.4). In the case at hand, zeros of
 are called radial caustic points and zeros of
are called radial caustic points and zeros of  are called tangential caustic points (see Figure 8).
By Equation (92), tangential caustic points occur if
are called tangential caustic points (see Figure 8).
By Equation (92), tangential caustic points occur if 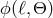 is a multiple of
is a multiple of  , i.e., whenever a light ray
crosses the axis of symmetry through the observer (see Figure 8). Symmetry implies that a point source is
seen as a ring (“Einstein ring”) if its worldline crosses a tangential caustic point. By contrast, a
point source whose wordline crosses a radial caustic point is seen infinitesimally extended in
the radial direction. The set of all tangential caustic points of the past light cone is called the
tangential caustic for short. In general, it has several connected components (“first, second,
etc. tangential caustic”). Each connected component is a spacelike curve in spacetime which projects to
(part of) the axis of symmetry through the observer. The radial caustic is a lightlike surface
in spacetime unless at points where it meets the axis; its projection to space is rotationally
symmetric around the axis. The best known example for a tangential caustic, with infinitely
many connected components, occurs in the Schwarzschild spacetime (see Figure 12). It is also
instructive to visualize radial and tangential caustics in terms of instantaneous wave fronts,
i.e., intersections of the light cone with hypersurfaces
, i.e., whenever a light ray
crosses the axis of symmetry through the observer (see Figure 8). Symmetry implies that a point source is
seen as a ring (“Einstein ring”) if its worldline crosses a tangential caustic point. By contrast, a
point source whose wordline crosses a radial caustic point is seen infinitesimally extended in
the radial direction. The set of all tangential caustic points of the past light cone is called the
tangential caustic for short. In general, it has several connected components (“first, second,
etc. tangential caustic”). Each connected component is a spacelike curve in spacetime which projects to
(part of) the axis of symmetry through the observer. The radial caustic is a lightlike surface
in spacetime unless at points where it meets the axis; its projection to space is rotationally
symmetric around the axis. The best known example for a tangential caustic, with infinitely
many connected components, occurs in the Schwarzschild spacetime (see Figure 12). It is also
instructive to visualize radial and tangential caustics in terms of instantaneous wave fronts,
i.e., intersections of the light cone with hypersurfaces  . Examples are shown in
Figures 13, 18, and 19. By symmetry, a tangential caustic point of an instantaneous wave front can
be neither a cusp nor a swallow-tail. Hence, the general result of Section 2.2 implies that the
tangential caustic is always unstable. The radial caustic in Figure 19 consists of cusps and is, thus,
stable.
. Examples are shown in
Figures 13, 18, and 19. By symmetry, a tangential caustic point of an instantaneous wave front can
be neither a cusp nor a swallow-tail. Hence, the general result of Section 2.2 implies that the
tangential caustic is always unstable. The radial caustic in Figure 19 consists of cusps and is, thus,
stable.
![]() ) with the general form (61
) with the general form (61![]() ) of a conformally stationary spacetime shows that
here the redshift potential
) of a conformally stationary spacetime shows that
here the redshift potential ![]() is a function of
is a function of ![]() only, the Fermat one-form
only, the Fermat one-form ![]() vanishes, and the Fermat
metric
vanishes, and the Fermat
metric ![]() is of the special form
is of the special form ![]() via
via ![]() can be written in terms
of integrals over the metric coefficients. We first restrict to the equatorial plane
can be written in terms
of integrals over the metric coefficients. We first restrict to the equatorial plane ![]() . The
. The
![]() -geodesics are then determined by the Lagrangian
-geodesics are then determined by the Lagrangian ![]() ] refers to a chosen observation event
] refers to a chosen observation event ![]() and a
chosen “source surface”
and a
chosen “source surface” ![]() . In general, for
. In general, for ![]() we may choose any 3-dimensional submanifold that is
ruled by timelike curves. The latter are to be interpreted as wordlines of light sources. In a spherically
symmetric and static spacetime, we may take advantage of the symmetry by choosing for
we may choose any 3-dimensional submanifold that is
ruled by timelike curves. The latter are to be interpreted as wordlines of light sources. In a spherically
symmetric and static spacetime, we may take advantage of the symmetry by choosing for ![]() a
sphere
a
sphere ![]() with its ruling by the
with its ruling by the ![]() -lines. This restricts the consideration to lensing for
static light sources. Note that all static light sources at radius
-lines. This restricts the consideration to lensing for
static light sources. Note that all static light sources at radius ![]() undergo the same redshift,
undergo the same redshift,
![]() . Without loss of generality, we place the observation event
. Without loss of generality, we place the observation event ![]() on the 3-axis
at radius
on the 3-axis
at radius ![]() . This gives us the past light cone in the representation (81
. This gives us the past light cone in the representation (81![]() ). To each ray from the
observer, with initial direction characterized by
). To each ray from the
observer, with initial direction characterized by ![]() , we can assign the total angle
, we can assign the total angle ![]() the ray
sweeps out on its way from
the ray
sweeps out on its way from ![]() to
to ![]() (see Figure 6
(see Figure 6![]() ).
). ![]() is given by Equation (86
is given by Equation (86![]() ),
),
![]() ,
, ![]() vanishes (see Sections 2.2, 2.3, and 2.4). In the case at hand, zeros of
vanishes (see Sections 2.2, 2.3, and 2.4). In the case at hand, zeros of
![]() are called radial caustic points and zeros of
are called radial caustic points and zeros of ![]() are called tangential caustic points (see Figure 8
are called tangential caustic points (see Figure 8![]() ).
By Equation (92
).
By Equation (92![]() ), tangential caustic points occur if
), tangential caustic points occur if ![]() is a multiple of
is a multiple of ![]() , i.e., whenever a light ray
crosses the axis of symmetry through the observer (see Figure 8
, i.e., whenever a light ray
crosses the axis of symmetry through the observer (see Figure 8![]() ). Symmetry implies that a point source is
seen as a ring (“Einstein ring”) if its worldline crosses a tangential caustic point. By contrast, a
point source whose wordline crosses a radial caustic point is seen infinitesimally extended in
the radial direction. The set of all tangential caustic points of the past light cone is called the
tangential caustic for short. In general, it has several connected components (“first, second,
etc. tangential caustic”). Each connected component is a spacelike curve in spacetime which projects to
(part of) the axis of symmetry through the observer. The radial caustic is a lightlike surface
in spacetime unless at points where it meets the axis; its projection to space is rotationally
symmetric around the axis. The best known example for a tangential caustic, with infinitely
many connected components, occurs in the Schwarzschild spacetime (see Figure 12
). Symmetry implies that a point source is
seen as a ring (“Einstein ring”) if its worldline crosses a tangential caustic point. By contrast, a
point source whose wordline crosses a radial caustic point is seen infinitesimally extended in
the radial direction. The set of all tangential caustic points of the past light cone is called the
tangential caustic for short. In general, it has several connected components (“first, second,
etc. tangential caustic”). Each connected component is a spacelike curve in spacetime which projects to
(part of) the axis of symmetry through the observer. The radial caustic is a lightlike surface
in spacetime unless at points where it meets the axis; its projection to space is rotationally
symmetric around the axis. The best known example for a tangential caustic, with infinitely
many connected components, occurs in the Schwarzschild spacetime (see Figure 12![]() ). It is also
instructive to visualize radial and tangential caustics in terms of instantaneous wave fronts,
i.e., intersections of the light cone with hypersurfaces
). It is also
instructive to visualize radial and tangential caustics in terms of instantaneous wave fronts,
i.e., intersections of the light cone with hypersurfaces ![]() . Examples are shown in
Figures 13
. Examples are shown in
Figures 13![]() , 18
, 18![]() , and 19
, and 19![]() . By symmetry, a tangential caustic point of an instantaneous wave front can
be neither a cusp nor a swallow-tail. Hence, the general result of Section 2.2 implies that the
tangential caustic is always unstable. The radial caustic in Figure 19
. By symmetry, a tangential caustic point of an instantaneous wave front can
be neither a cusp nor a swallow-tail. Hence, the general result of Section 2.2 implies that the
tangential caustic is always unstable. The radial caustic in Figure 19![]() consists of cusps and is, thus,
stable.
consists of cusps and is, thus,
stable.