4.1 Dynamics of a massive binary in a fixed stellar background
Stars passing within a distance  of the center of mass of a hard binary undergo a
complex interaction with the two black holes, followed almost always by ejection at velocity
of the center of mass of a hard binary undergo a
complex interaction with the two black holes, followed almost always by ejection at velocity
 , the “gravitational slingshot” [191
, the “gravitational slingshot” [191 ]. Each ejected star carries away energy and angular
momentum, causing the semi-major axis, eccentricity, orientation, and center-of-mass velocity of the
binary to change and the local density of stars to drop. If the stellar distribution is assumed
fixed far from the binary and if the contribution to the potential from the stars is ignored, the
rate at which these changes occur can be computed by carrying out scattering experiments of
massless stars against a binary whose orbital elements remain fixed during each interaction
[89
]. Each ejected star carries away energy and angular
momentum, causing the semi-major axis, eccentricity, orientation, and center-of-mass velocity of the
binary to change and the local density of stars to drop. If the stellar distribution is assumed
fixed far from the binary and if the contribution to the potential from the stars is ignored, the
rate at which these changes occur can be computed by carrying out scattering experiments of
massless stars against a binary whose orbital elements remain fixed during each interaction
[89 , 187, 87
, 187, 87 , 88
, 88 , 13, 148
, 13, 148 , 177
, 177 , 133
, 133 , 134
, 134 ]. Figure 4 shows an example of field star velocity changes in a set
of scattering experiments.
Consider an encounter of a single field star of mass
]. Figure 4 shows an example of field star velocity changes in a set
of scattering experiments.
Consider an encounter of a single field star of mass 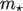 with the binary. Long before the encounter, the
field star has velocity
with the binary. Long before the encounter, the
field star has velocity  with respect to the center of mass of the field star-binary system and its impact
parameter is
with respect to the center of mass of the field star-binary system and its impact
parameter is  . A long time after the encounter, the velocity
. A long time after the encounter, the velocity  of the field star attains a constant value.
Conservation of linear momentum implies that the change
of the field star attains a constant value.
Conservation of linear momentum implies that the change  in the velocity of the binary’s center of
mass is given by
The velocity change results in a random walk of the binary’s center-of-mass momentum, as discussed in
more detail below. The energy of the field star-binary system, expressed in terms of pre-encounter
quantities, is
with
in the velocity of the binary’s center of
mass is given by
The velocity change results in a random walk of the binary’s center-of-mass momentum, as discussed in
more detail below. The energy of the field star-binary system, expressed in terms of pre-encounter
quantities, is
with  the initial velocity of the binary’s center of mass and
the initial velocity of the binary’s center of mass and  the binary’s initial
semi-major axis. After the encounter,
and
the binary’s initial
semi-major axis. After the encounter,
and  , so that
Averaged over a distribution of field-star velocities and directions, Equation (14) gives the binary hardening
rate
, so that
Averaged over a distribution of field-star velocities and directions, Equation (14) gives the binary hardening
rate  [87
[87 , 88, 148
, 88, 148 , 177
, 177 ].
].
The angular momentum of the field star-binary system about its center of mass, expressed in terms of
pre-encounter quantities, is
where  and
and  with
with  the binary’s orbital angular momentum. Conservation of
angular momentum during the encounter gives
Changes in
the binary’s orbital angular momentum. Conservation of
angular momentum during the encounter gives
Changes in  correspond to changes in the binary’s orbital eccentricity
correspond to changes in the binary’s orbital eccentricity  via the relation
via the relation
 [148
[148 , 177
, 177 ]. Changes in the direction of
]. Changes in the direction of  correspond to changes in the
orientation of the binary [134
correspond to changes in the
orientation of the binary [134 ].
].
The results of the scattering experiments can be summarized via a set of dimensionless coefficients
 which define the mean rates of change of the parameters characterizing the binary and the
stellar background. These coefficients are functions of the binary mass ratio, eccentricity and hardness but
are typically independent of
which define the mean rates of change of the parameters characterizing the binary and the
stellar background. These coefficients are functions of the binary mass ratio, eccentricity and hardness but
are typically independent of  in the limit that the binary is very hard. The hardening rate of the binary
is given by
in the limit that the binary is very hard. The hardening rate of the binary
is given by
with  and
and  the density and 1D velocity dispersion of stars at infinity. The mass ejection rate is
with
the density and 1D velocity dispersion of stars at infinity. The mass ejection rate is
with  the mass in stars that escape the binary. The rate of change of the binary’s orbital eccentricity
is
The diffusion coefficient describing changes in the binary’s orientation is
with
the mass in stars that escape the binary. The rate of change of the binary’s orbital eccentricity
is
The diffusion coefficient describing changes in the binary’s orientation is
with  the stellar mass. Brownian motion of the binary’s center of mass is determined by the
coefficients
the stellar mass. Brownian motion of the binary’s center of mass is determined by the
coefficients  and
and  which characterize the Chandrasekhar diffusion coefficients at low
which characterize the Chandrasekhar diffusion coefficients at low  :
The mean square velocity of the binary’s center of mass is
:
The mean square velocity of the binary’s center of mass is  .
.
The binary hardening coefficient  reaches a constant value of
reaches a constant value of  in the limit
in the limit 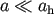 , with a
weak dependence on
, with a
weak dependence on  [87, 148
[87, 148 , 177
, 177 ]. In a fixed background, Equation (17) therefore implies that a hard
binary hardens at a constant rate:
]. In a fixed background, Equation (17) therefore implies that a hard
binary hardens at a constant rate:
This is sometimes taken as the definition of a “hard binary”. The time to reach zero separation is
Orbital shrinkage would occur quite rapidly in the environment of a galactic nucleus if the properties of the
stellar background remained fixed.
However if the binary manages to shrink to a separation at which  , the changes it induces
in its stellar surroundings will be considerable. The mass ejected by the binary in decaying from
, the changes it induces
in its stellar surroundings will be considerable. The mass ejected by the binary in decaying from  to
to
 is given by the integral of Equation (18):
is given by the integral of Equation (18):
Figure 5 shows  as a function of the mass ratio
as a function of the mass ratio  for
for 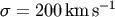 and various values of
and various values of  .
The mass ejected in reaching coalescence is of order
.
The mass ejected in reaching coalescence is of order  for equal-mass binaries, and several
times
for equal-mass binaries, and several
times  when
when  . A SBH that grew to its current size through a succession of
mergers should therefore have displaced a few times its own mass in stars. If this mass came
mostly from stars that were originally in the nucleus, the density within
. A SBH that grew to its current size through a succession of
mergers should therefore have displaced a few times its own mass in stars. If this mass came
mostly from stars that were originally in the nucleus, the density within  would drop
drastically and the hardening would stop. Without some way of replenishing the supply of stars
(and in the absence of other mechanisms for extracting angular momentum from the binary,
e.g. torques from gas clouds; cf. Section 8), decay would stall at a separation much greater than
would drop
drastically and the hardening would stop. Without some way of replenishing the supply of stars
(and in the absence of other mechanisms for extracting angular momentum from the binary,
e.g. torques from gas clouds; cf. Section 8), decay would stall at a separation much greater than
 .
In the case of extreme binary mass ratios,
.
In the case of extreme binary mass ratios,  , the assumption that all stars passing a distance
, the assumption that all stars passing a distance
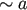 from the binary will be ejected is likely to be incorrect; many such stars will pass through the binary
system without being appreciably perturbed by the smaller black hole. The concept of “ejection” in extreme
binary mass ratios may be misleading; since the typical amount of energy transferred in stellar
pericenter passages is small, most of the slingshot stars are not ejected from the nucleus and remain
bound to the larger black hole. Figure 5 should thus be interpreted with caution in the regime
from the binary will be ejected is likely to be incorrect; many such stars will pass through the binary
system without being appreciably perturbed by the smaller black hole. The concept of “ejection” in extreme
binary mass ratios may be misleading; since the typical amount of energy transferred in stellar
pericenter passages is small, most of the slingshot stars are not ejected from the nucleus and remain
bound to the larger black hole. Figure 5 should thus be interpreted with caution in the regime
 . The extreme-mass-ratio regime is poorly understood but deserves more study in view
of the possibility that intermediate-mass black holes may exist having masses of
. The extreme-mass-ratio regime is poorly understood but deserves more study in view
of the possibility that intermediate-mass black holes may exist having masses of  [43].
[43].
Changes in the binary’s orbital eccentricity (Equation 19) are potentially important because the gravity
wave coalescence time drops rapidly as 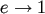 (Equation 8). For a hard binary, scattering experiments
give
(Equation 8). For a hard binary, scattering experiments
give  , with
, with  for an equal-mass binary [148, 177
for an equal-mass binary [148, 177 ]. The dependence of
]. The dependence of 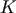 on
on  is not well understood and is an important topic for further study. The implied
changes in
is not well understood and is an important topic for further study. The implied
changes in  as a binary decays from
as a binary decays from  to zero are modest,
to zero are modest,  , for all initial
eccentricities.
, for all initial
eccentricities.
![]() which define the mean rates of change of the parameters characterizing the binary and the
stellar background. These coefficients are functions of the binary mass ratio, eccentricity and hardness but
are typically independent of
which define the mean rates of change of the parameters characterizing the binary and the
stellar background. These coefficients are functions of the binary mass ratio, eccentricity and hardness but
are typically independent of ![]() in the limit that the binary is very hard. The hardening rate of the binary
is given by
in the limit that the binary is very hard. The hardening rate of the binary
is given by ![]() reaches a constant value of
reaches a constant value of ![]() in the limit
in the limit ![]() , with a
weak dependence on
, with a
weak dependence on ![]() [87, 148
[87, 148![]() , 177
, 177![]() ]. In a fixed background, Equation (17
]. In a fixed background, Equation (17![]() ) therefore implies that a hard
binary hardens at a constant rate:
) therefore implies that a hard
binary hardens at a constant rate: ![]() , the changes it induces
in its stellar surroundings will be considerable. The mass ejected by the binary in decaying from
, the changes it induces
in its stellar surroundings will be considerable. The mass ejected by the binary in decaying from ![]() to
to
![]() is given by the integral of Equation (18
is given by the integral of Equation (18![]() ):
): ![]() ) are potentially important because the gravity
wave coalescence time drops rapidly as
) are potentially important because the gravity
wave coalescence time drops rapidly as ![]() (Equation 8
(Equation 8![]() ). For a hard binary, scattering experiments
give
). For a hard binary, scattering experiments
give ![]() , with
, with ![]() for an equal-mass binary [148, 177
for an equal-mass binary [148, 177![]() ]. The dependence of
]. The dependence of ![]() on
on ![]() is not well understood and is an important topic for further study. The implied
changes in
is not well understood and is an important topic for further study. The implied
changes in ![]() as a binary decays from
as a binary decays from ![]() to zero are modest,
to zero are modest, ![]() , for all initial
eccentricities.
, for all initial
eccentricities.