9 Spin Evolution during Mergers
Coalescence of a binary black hole results in a spinning
remnant.
Angular momentum conservation implies
where  and
and  are the spin angular momenta of the two SBHs just before the final plunge,
are the spin angular momenta of the two SBHs just before the final plunge,
 is the orbital angular momentum of the binary before the plunge,
is the orbital angular momentum of the binary before the plunge,  is the spin of the
resulting black hole, and
is the spin of the
resulting black hole, and 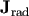 is the angular momentum carried away by gravitational waves
during and after the coalescence [54]. The simplest case to treat is extreme mass ratio mergers,
is the angular momentum carried away by gravitational waves
during and after the coalescence [54]. The simplest case to treat is extreme mass ratio mergers,
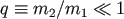 , for which the binary can be described as a test particle of mass
, for which the binary can be described as a test particle of mass  orbiting a
black hole of mass
orbiting a
black hole of mass  , and both
, and both  and
and  can be ignored. The change
in the larger hole’s spin is computed by adding the smaller hole’s energy and orbital angular
momentum at the last stable orbit (LSO). The latter varies from
can be ignored. The change
in the larger hole’s spin is computed by adding the smaller hole’s energy and orbital angular
momentum at the last stable orbit (LSO). The latter varies from  for circular
equatorial orbits around a non-spinning hole to
for circular
equatorial orbits around a non-spinning hole to  for prograde (retrograde) orbits
around a maximally-spinning hole,
for prograde (retrograde) orbits
around a maximally-spinning hole,  . The much larger value of
. The much larger value of  in the case
of retrograde capture implies that a rapidly-rotating hole will typically spin down if capture
occurs from random directions [34, 69, 226, 227
in the case
of retrograde capture implies that a rapidly-rotating hole will typically spin down if capture
occurs from random directions [34, 69, 226, 227 , 91
, 91 ]. The change in spin assuming
]. The change in spin assuming  is
where
is
where  ,
,  is the orbital angular momentum parallel to
is the orbital angular momentum parallel to  , and
, and  . The first
term in Equation (49) describes conservation of spin angular momentum of the larger hole as its mass
grows,
. The first
term in Equation (49) describes conservation of spin angular momentum of the larger hole as its mass
grows,  , while the second term describes the increase in spin due to torquing by the smaller
body.
The change in spin after a single coalescence is illustrated in Figure 13 as a function of
, while the second term describes the increase in spin due to torquing by the smaller
body.
The change in spin after a single coalescence is illustrated in Figure 13 as a function of  and initial
spin; the upper (lower) curves represent prograde (retrograde) captures from equatorial orbits, and the
dashed lines are for capture over the pole. The bias toward spin-down is evident; retrograde capture from
the equatorial plane produces a nearly (but never completely) non-spinning remnant when
and initial
spin; the upper (lower) curves represent prograde (retrograde) captures from equatorial orbits, and the
dashed lines are for capture over the pole. The bias toward spin-down is evident; retrograde capture from
the equatorial plane produces a nearly (but never completely) non-spinning remnant when  ,
,
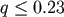 , and rapid final rotation (
, and rapid final rotation (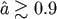 ) requires both a large initial spin and a favorable inclination.
On the other hand, if the larger hole is slowly rotating initially,
) requires both a large initial spin and a favorable inclination.
On the other hand, if the larger hole is slowly rotating initially, 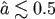 , mass ratios
, mass ratios  always result in spin-up. The oft-repeated statement that “mergers spin down black holes”
reflects a preconception that SBHs are likely to be formed in a state of near-maximal rotation
(e.g. [14
always result in spin-up. The oft-repeated statement that “mergers spin down black holes”
reflects a preconception that SBHs are likely to be formed in a state of near-maximal rotation
(e.g. [14 , 61]).
Successive mergers from random directions with fixed
, 61]).
Successive mergers from random directions with fixed  (i.e. secondary mass grows proportionately to
primary mass) lead to a steady-state spin distribution
(i.e. secondary mass grows proportionately to
primary mass) lead to a steady-state spin distribution  that is uniquely determined
by
that is uniquely determined
by  . For small
. For small  , this distribution can be derived from the Fokker-Planck equation [91]:
Figure 14 shows
, this distribution can be derived from the Fokker-Planck equation [91]:
Figure 14 shows  for various values of
for various values of 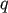 , computed via Monte-Carlo experiments (not from the
Fokker-Planck equation) using the test-mass approximation for
, computed via Monte-Carlo experiments (not from the
Fokker-Planck equation) using the test-mass approximation for  . The Gaussian form of
Equation (50) is seen to be accurate only for
. The Gaussian form of
Equation (50) is seen to be accurate only for  . For
. For  , the distribution is skewed toward
large spins.
Accurate calculation of spin-up during a merger of comparably massive black holes requires a fully
general-relativistic numerical treatment. Adopting various approximations for the radius of the innermost
stable circular orbit (ISCO) for comparably massive binaries [28, 17, 80, 31], and assuming that mass and
angular momenta are conserved during coalescence, gives a remnant spin in equal-mass mergers of
, the distribution is skewed toward
large spins.
Accurate calculation of spin-up during a merger of comparably massive black holes requires a fully
general-relativistic numerical treatment. Adopting various approximations for the radius of the innermost
stable circular orbit (ISCO) for comparably massive binaries [28, 17, 80, 31], and assuming that mass and
angular momenta are conserved during coalescence, gives a remnant spin in equal-mass mergers of
 . Baker et al. [9, 10] present full numerical calculations of equal-mass mergers with and
without initial spins. In the absence of initial spins, 3% of the system’s mass-energy and 12% of its angular
momentum are lost to gravitational radiation, and the final spin is
. Baker et al. [9, 10] present full numerical calculations of equal-mass mergers with and
without initial spins. In the absence of initial spins, 3% of the system’s mass-energy and 12% of its angular
momentum are lost to gravitational radiation, and the final spin is  . Coalescence of initially
spinning holes from circular orbits in the equatorial plane yields
. Coalescence of initially
spinning holes from circular orbits in the equatorial plane yields  with
with  the initial
spin parameter of the two holes (assumed equal); Baker et al. considered initial spins in the
range
the initial
spin parameter of the two holes (assumed equal); Baker et al. considered initial spins in the
range  , where negative/positive values indicate spins aligned/counteraligned
with the orbital angular momentum. Extrapolating this result toward
, where negative/positive values indicate spins aligned/counteraligned
with the orbital angular momentum. Extrapolating this result toward  suggests that
prograde mergers of black holes with initial spins
suggests that
prograde mergers of black holes with initial spins  will result in a maximally-spinning
remnant.
will result in a maximally-spinning
remnant.
Confronting these predictions with observation is problematic for a number of reasons: Merger histories
of observed SBHs are not known, SBH spins are difficult to determine observationally, and other
mechanisms, such as gas accretion, can act efficiently to spin up SBHs [14]. However there is circumstantial
evidence that mergers played a dominant role in determining the spins of at least some SBH. If
SBH spins were the product of gas accretion, the jets in active galaxies should point nearly
perpendicularly to the disks of their host galaxies [182]. In fact, there is almost no correlation
between jet direction and galaxy major axis in Seyfert galaxies [211, 101 , 194]. Among the
possible explanations [101] for the misalignment, perhaps the most natural is that SBH spins were
determined by the same merger events that formed the bulge, long before the formation of the
gaseous disk, and that subsequent spin-up by gas accretion from the disk plane has been minimal
[134
, 194]. Among the
possible explanations [101] for the misalignment, perhaps the most natural is that SBH spins were
determined by the same merger events that formed the bulge, long before the formation of the
gaseous disk, and that subsequent spin-up by gas accretion from the disk plane has been minimal
[134 ].
].
Coalescence of two black holes during a merger should result in a “spin-flip”, a reorientation of the
spin axis of the more massive black hole. In the test-particle limit, the reorientation angle is
with  the cosine of the angle between the orbital angular momentum vector and the spin axis of the
larger hole. When
the cosine of the angle between the orbital angular momentum vector and the spin axis of the
larger hole. When  , the spin orientation is overwhelmed by the plunging body in a retrograde
merger, even if the initial spin of the larger hole was close to maximal. Hence, even “minor
mergers” (defined, following galactic dynamicists, as mergers with
, the spin orientation is overwhelmed by the plunging body in a retrograde
merger, even if the initial spin of the larger hole was close to maximal. Hence, even “minor
mergers” (defined, following galactic dynamicists, as mergers with  ) are able to produce a
substantial reorientation. In fact there is a class of active galaxies which exhibit radio lobes at two,
nearly-orthogonal orientations, and in which the production of plasma along the fainter lobes
appears to have ceased [115, 32]. These “X-shaped” or “winged” radio galaxies, of which about a
dozen are known, are plausible sites of recent (within the last
) are able to produce a
substantial reorientation. In fact there is a class of active galaxies which exhibit radio lobes at two,
nearly-orthogonal orientations, and in which the production of plasma along the fainter lobes
appears to have ceased [115, 32]. These “X-shaped” or “winged” radio galaxies, of which about a
dozen are known, are plausible sites of recent (within the last 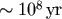 ) black-hole coalescence
[137
) black-hole coalescence
[137 , 233]. Furthermore the implied coalescence rate is roughly consistent with the expected
merger rate for the host galaxies of luminous radio sources [137
, 233]. Furthermore the implied coalescence rate is roughly consistent with the expected
merger rate for the host galaxies of luminous radio sources [137 ]. Alternative models have been
proposed for the X-shaped sources, including a warping instability of accretion disks [174],
backflow of gas along the active lobes [116], and binary-disk interactions before coalescence
[120].
It is likely that all of these mechanisms are active at some level and that the time scale for realignment
influences the radio source morphology, with the most rapid realignments producing the classical X-shaped
sources, while slower realignment would cause the jet to deposit its energy into a large volume, leading to an
S-shaped FRI radio source [137].
If the black holes are spinning prior to coalescence, they will experience spin-orbit precession, on a time
scale that is intermediate between
]. Alternative models have been
proposed for the X-shaped sources, including a warping instability of accretion disks [174],
backflow of gas along the active lobes [116], and binary-disk interactions before coalescence
[120].
It is likely that all of these mechanisms are active at some level and that the time scale for realignment
influences the radio source morphology, with the most rapid realignments producing the classical X-shaped
sources, while slower realignment would cause the jet to deposit its energy into a large volume, leading to an
S-shaped FRI radio source [137].
If the black holes are spinning prior to coalescence, they will experience spin-orbit precession, on a time
scale that is intermediate between  and the orbital period. To PN2.5 order, the spin angular
momentum of either hole evolves as [98]
where
and the orbital period. To PN2.5 order, the spin angular
momentum of either hole evolves as [98]
where  is a unit vector in the direction of the displacement vector between the two black
holes. The evolution equation for
is a unit vector in the direction of the displacement vector between the two black
holes. The evolution equation for  is given by interchanging the indices. The magnitude of
each spin vector remains fixed (to this order), and each spin precesses around the total angular
momentum vector
is given by interchanging the indices. The magnitude of
each spin vector remains fixed (to this order), and each spin precesses around the total angular
momentum vector  . When the two black holes are comparably massive, the
orbital angular momentum greatly exceeds the spin angular momentum of either hole until
just prior to coalescence. As the binary shrinks, the spins have a tendency to unalign with
. When the two black holes are comparably massive, the
orbital angular momentum greatly exceeds the spin angular momentum of either hole until
just prior to coalescence. As the binary shrinks, the spins have a tendency to unalign with
 . Ignoring spin-spin effects, the precession rate for equal-mass holes in a circular orbit is
The precession rate is lower than the orbital frequency:
where
. Ignoring spin-spin effects, the precession rate for equal-mass holes in a circular orbit is
The precession rate is lower than the orbital frequency:
where  , but higher than the radiation reaction time scale:
unless the binary is close to coalescence. If the dominant source of energy loss during the late stages of infall
is gravitational radiation, the spin direction will undergo many cycles of precession before the black holes
coalesce. This does not seem to happen in the X-shaped radio sources, based on the apparently sudden
change in jet direction; if the coalescence model for the X-sources is correct, the final stages of infall must
occur on a shorter time scale than
, but higher than the radiation reaction time scale:
unless the binary is close to coalescence. If the dominant source of energy loss during the late stages of infall
is gravitational radiation, the spin direction will undergo many cycles of precession before the black holes
coalesce. This does not seem to happen in the X-shaped radio sources, based on the apparently sudden
change in jet direction; if the coalescence model for the X-sources is correct, the final stages of infall must
occur on a shorter time scale than  . This might be seen as evidence that shrinkage of the
binary is usually driven by gas dynamics, not gravitational radiation losses, prior to the final
coalescence.
. This might be seen as evidence that shrinkage of the
binary is usually driven by gas dynamics, not gravitational radiation losses, prior to the final
coalescence.
When the black hole masses are very different,  , the ratio of spin of the larger hole to
, the ratio of spin of the larger hole to  is
is
where 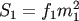 . The two quantities are approximately equal when the separation measured in units of
the larger hole’s Schwarzschild radius is equal to
. The two quantities are approximately equal when the separation measured in units of
the larger hole’s Schwarzschild radius is equal to  . When this separation is reached, the binary orbit
rapidly changes its plane, and a new regime is reached where the spin of the smaller black hole
precesses about the spin of the larger hole. The precession rate of the larger hole is given by
in both regimes, and
. When this separation is reached, the binary orbit
rapidly changes its plane, and a new regime is reached where the spin of the smaller black hole
precesses about the spin of the larger hole. The precession rate of the larger hole is given by
in both regimes, and
The spin direction of a black hole formed via binary coalescence is also affected by torques that reorient
the binary prior to coalescence. The role of torques from gaseous accretion disks was discussed above;
another source of torques is perturbations from passing stars or gas clouds [134 ]. A single star that passes
within a distance
]. A single star that passes
within a distance  of the binary will exchange orbital angular momentum with it, leading both to a
change in the binary’s orbital eccentricity as well as a change in the orientation of the binary’s spin axis, as
discussed above. Referring to Equations (17) and (20), the reorientation rate is related to the hardening
rate via
of the binary will exchange orbital angular momentum with it, leading both to a
change in the binary’s orbital eccentricity as well as a change in the orientation of the binary’s spin axis, as
discussed above. Referring to Equations (17) and (20), the reorientation rate is related to the hardening
rate via
where  . Scattering experiments [134] give
. Scattering experiments [134] give  for a hard, equal-mass binary.
The implied change in the binary’s orientation after shrinking from
for a hard, equal-mass binary.
The implied change in the binary’s orientation after shrinking from  to
to  is
The reorientation begins to be significant if
is
The reorientation begins to be significant if  , which may be the case for intermediate-mass
black holes.
, which may be the case for intermediate-mass
black holes.
![]() , 194]. Among the
possible explanations [101] for the misalignment, perhaps the most natural is that SBH spins were
determined by the same merger events that formed the bulge, long before the formation of the
gaseous disk, and that subsequent spin-up by gas accretion from the disk plane has been minimal
[134
, 194]. Among the
possible explanations [101] for the misalignment, perhaps the most natural is that SBH spins were
determined by the same merger events that formed the bulge, long before the formation of the
gaseous disk, and that subsequent spin-up by gas accretion from the disk plane has been minimal
[134![]() ].
].
![]() , the ratio of spin of the larger hole to
, the ratio of spin of the larger hole to ![]() is
is
![]() ]. A single star that passes
within a distance
]. A single star that passes
within a distance ![]() of the binary will exchange orbital angular momentum with it, leading both to a
change in the binary’s orbital eccentricity as well as a change in the orientation of the binary’s spin axis, as
discussed above. Referring to Equations (17
of the binary will exchange orbital angular momentum with it, leading both to a
change in the binary’s orbital eccentricity as well as a change in the orientation of the binary’s spin axis, as
discussed above. Referring to Equations (17![]() ) and (20
) and (20![]() ), the reorientation rate is related to the hardening
rate via
), the reorientation rate is related to the hardening
rate via