6  -Body Studies of Binary Black Hole Evolution
-Body Studies of Binary Black Hole Evolution
The interaction of a massive binary with point perturbers at the center of a galaxy is a
straightforward problem for  -body simulation. In principle,
-body simulation. In principle,  -body studies can reveal
both the long-term evolution of the binary, as well as the effect of the binary on its stellar
surroundings. The latter can be compared with observed nuclear density profiles as a test of the theory
(Section 7).
-body studies can reveal
both the long-term evolution of the binary, as well as the effect of the binary on its stellar
surroundings. The latter can be compared with observed nuclear density profiles as a test of the theory
(Section 7).
Unfortunately, unless great care is taken,  -body studies are likely to give misleading results. This
follows from the result (Section 4.3) that time scales for two-body scattering of stars into the binary’s loss
cone are of order
-body studies are likely to give misleading results. This
follows from the result (Section 4.3) that time scales for two-body scattering of stars into the binary’s loss
cone are of order  or somewhat longer in real galaxies. In
or somewhat longer in real galaxies. In  -body simulations, relaxation times
are shorter by factors of
-body simulations, relaxation times
are shorter by factors of  than in real galaxies, hence the long-term evolution of the binary is
likely to be dominated by spurious loss cone refilling, wandering of the binary, and other noise-driven
effects.
than in real galaxies, hence the long-term evolution of the binary is
likely to be dominated by spurious loss cone refilling, wandering of the binary, and other noise-driven
effects.
 -body studies are most useful at characterizing the early stages of binary formation and decay, or
simulating the disruptive tidal effects of a SBH on the nucleus of an infalling galaxy. Due to algorithmic
limitations - primarily the difficulty of integrating galaxy models with high central concentrations - most
such studies [35, 75, 126, 125, 158, 157, 86
-body studies are most useful at characterizing the early stages of binary formation and decay, or
simulating the disruptive tidal effects of a SBH on the nucleus of an infalling galaxy. Due to algorithmic
limitations - primarily the difficulty of integrating galaxy models with high central concentrations - most
such studies [35, 75, 126, 125, 158, 157, 86 , 25
, 25 , 128
, 128 ] have been based on galaxy models with
unrealistically large cores.
] have been based on galaxy models with
unrealistically large cores.
Figure 7 is from the first [136 ]
]  -body simulation of galaxy mergers in which the pre-merger galaxies
contained power-law nuclear cusps as well as massive particles representing the SBHs. These simulations
were run using GADGET [202], a tree code with inter-particle softening, and were not able to accurately follow
the formation and decay of the massive binary. The SBH in the larger galaxy was found to tidally disrupt
the steep cusp in the infalling galaxy, producing a remnant with only slightly higher central density than
that of the giant galaxy initially. This result helps to explain the absence of dense cusps in bright galaxies
[55], and suggests that the central structure of galaxies can only be understood by taking into account the
destructive influence of SBHs on the stellar distribution during mergers. Additional results, using a
similar
-body simulation of galaxy mergers in which the pre-merger galaxies
contained power-law nuclear cusps as well as massive particles representing the SBHs. These simulations
were run using GADGET [202], a tree code with inter-particle softening, and were not able to accurately follow
the formation and decay of the massive binary. The SBH in the larger galaxy was found to tidally disrupt
the steep cusp in the infalling galaxy, producing a remnant with only slightly higher central density than
that of the giant galaxy initially. This result helps to explain the absence of dense cusps in bright galaxies
[55], and suggests that the central structure of galaxies can only be understood by taking into account the
destructive influence of SBHs on the stellar distribution during mergers. Additional results, using a
similar  -body code and a variety of mass ratios for the merging galaxies, were reported in
[141].
-body code and a variety of mass ratios for the merging galaxies, were reported in
[141].
Had these simulations been extended to longer times using a more accurate  -body code,
the massive binary would have ejected stars via the gravitational slingshot and lowered the
central density still more. This was first demonstrated [150
-body code,
the massive binary would have ejected stars via the gravitational slingshot and lowered the
central density still more. This was first demonstrated [150 ] in an
] in an  -body study that used a
tree code for the early stages of the merger, and NBODY6, a high-precision, direct-summation
code [1], for the later stages, when the binary separation fell below the tree code’s softening
length. The pre-merger galaxies had steep,
-body study that used a
tree code for the early stages of the merger, and NBODY6, a high-precision, direct-summation
code [1], for the later stages, when the binary separation fell below the tree code’s softening
length. The pre-merger galaxies had steep,  density cusps and the mass ratio was 1:1.
These simulations were continued until the binary separation had decayed by a factor of
density cusps and the mass ratio was 1:1.
These simulations were continued until the binary separation had decayed by a factor of  10
below
10
below  . The initially steep nuclear cusps were converted to shallower,
. The initially steep nuclear cusps were converted to shallower,  profiles
shortly after the SBH particles had formed a hard binary; thereafter the nuclear profile evolved
slowly toward even shallower slopes as the massive binary ejected stars. As Figure 7 illustrates,
the stellar density around the binary drops very quickly after the binary reaches a separation
profiles
shortly after the SBH particles had formed a hard binary; thereafter the nuclear profile evolved
slowly toward even shallower slopes as the massive binary ejected stars. As Figure 7 illustrates,
the stellar density around the binary drops very quickly after the binary reaches a separation
 .
The hardening rate of the binary in these simulations was found not to be strongly dependent on the
number of particles. This result was subsequently shown [152
.
The hardening rate of the binary in these simulations was found not to be strongly dependent on the
number of particles. This result was subsequently shown [152 ] to be due to the small
] to be due to the small  : Stars were
resupplied to the loss cone via collisions at a higher rate than they were being kicked out by the binary,
ensuring a continuous supply of stars and allowing the binary to continue to shrink. While a
qualitatively similar evolution may take place in some galaxies - for instance, loss cones in
non-axisymmetric potentials can be continuously repopulated by stars on centrophilic orbits
(Section 4.4) - collisional loss cone refilling is very unlikely to achieve anything like a full loss
cone except in very small, dense galaxies. The long-term evolution of the binary in almost all
published
: Stars were
resupplied to the loss cone via collisions at a higher rate than they were being kicked out by the binary,
ensuring a continuous supply of stars and allowing the binary to continue to shrink. While a
qualitatively similar evolution may take place in some galaxies - for instance, loss cones in
non-axisymmetric potentials can be continuously repopulated by stars on centrophilic orbits
(Section 4.4) - collisional loss cone refilling is very unlikely to achieve anything like a full loss
cone except in very small, dense galaxies. The long-term evolution of the binary in almost all
published  -body simulations are therefore not representative of what one would expect in real
galaxies.
The relevant dimensionless parameter is
where
-body simulations are therefore not representative of what one would expect in real
galaxies.
The relevant dimensionless parameter is
where  is the change over one radial period in the angular momentum of a star on a low-
is the change over one radial period in the angular momentum of a star on a low- orbit, and
orbit, and
 is the angular momentum of an orbit at the edge of the binary’s loss cone. A value
is the angular momentum of an orbit at the edge of the binary’s loss cone. A value  implies
that the loss cone orbits at energy
implies
that the loss cone orbits at energy  are re-populated at a much higher rate than they are
de-populated by the binary, and the loss cone remains nearly full. A value
are re-populated at a much higher rate than they are
de-populated by the binary, and the loss cone remains nearly full. A value 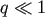 implies that the
loss cone is essentially empty, and repopulation must take place diffusively, as stars scatter in
from
implies that the
loss cone is essentially empty, and repopulation must take place diffusively, as stars scatter in
from 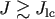 . In real galaxies,
. In real galaxies,  is large and
is large and 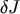 is small, implying
is small, implying  . Achieving
. Achieving
 in
in 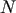 -body simulations requires large particle numbers, and/or a model for the galaxy
that has an unrealistically low central density, so that the star-star relaxation time is long.
Figure 9 shows a recent set of
-body simulations requires large particle numbers, and/or a model for the galaxy
that has an unrealistically low central density, so that the star-star relaxation time is long.
Figure 9 shows a recent set of  -body simulations that does both [20]. The massive binary
was embedded in a Plummer [168] galaxy model, which has a core radius comparable to its
half-mass radius; this model is very different from real galaxies but its very low degree of central
concentration implies a long relaxation time and low rate of collisional loss-cone refilling. Large
particle numbers were achieved, without sacrificing accuracy, by running the simulation on a
parallel GRAPE cluster. The
-body simulations that does both [20]. The massive binary
was embedded in a Plummer [168] galaxy model, which has a core radius comparable to its
half-mass radius; this model is very different from real galaxies but its very low degree of central
concentration implies a long relaxation time and low rate of collisional loss-cone refilling. Large
particle numbers were achieved, without sacrificing accuracy, by running the simulation on a
parallel GRAPE cluster. The  -dependence of the binary’s hardening rate is clear; in the
simulations with binary mass
-dependence of the binary’s hardening rate is clear; in the
simulations with binary mass  , the
, the 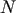 -dependence of the hardening
rate is
-dependence of the hardening
rate is  , almost as steep as the
, almost as steep as the  dependence predicted for an
“empty” loss cone [152
dependence predicted for an
“empty” loss cone [152 ]. A similar study [128
]. A similar study [128 ], based on King-model galaxies, found a similar
result.
], based on King-model galaxies, found a similar
result.
The Plummer-model initial conditions used in the simulations of Figure 9 were identical to those
adopted in two other  -body studies based on a more approximate
-body studies based on a more approximate  -body code [178
-body code [178 , 25].
Contrary to Figure 9, Chatterjee, Hernquist & Loeb (2003) found that the binary hardening
rate “saturated” at values of
, 25].
Contrary to Figure 9, Chatterjee, Hernquist & Loeb (2003) found that the binary hardening
rate “saturated” at values of  , remaining constant up to
, remaining constant up to  . They
speculated that this was due to a kind of Brownian-motion-mediated feedback, in which the
binary maintains a constant supply rate by modulating the local density of stars. However
no supporting evidence for this model was presented; for instance, it was not demonstrated
that the central density was actually regulated by the binary, or that the amplitude of the
Brownian wandering increased with
. They
speculated that this was due to a kind of Brownian-motion-mediated feedback, in which the
binary maintains a constant supply rate by modulating the local density of stars. However
no supporting evidence for this model was presented; for instance, it was not demonstrated
that the central density was actually regulated by the binary, or that the amplitude of the
Brownian wandering increased with  in the manner postulated. Furthermore these authors
provided no plots showing the claimed
in the manner postulated. Furthermore these authors
provided no plots showing the claimed  -dependence of the hardening rate. Chatterjee et al.’s
conclusion, that “a substantial fraction of all massive binaries in galaxies can coalesce within
a Hubble time”, is not substantiated by the more accurate
-dependence of the hardening rate. Chatterjee et al.’s
conclusion, that “a substantial fraction of all massive binaries in galaxies can coalesce within
a Hubble time”, is not substantiated by the more accurate  -body simulations shown in
Figure 9.
-body simulations shown in
Figure 9.
While Brownian motion probably does affect the decay rate of binaries in  -body simulations [152
-body simulations [152 ], it
is doubtful that the effect is significant in real galaxies. The Brownian velocity of single black holes is found
in
], it
is doubtful that the effect is significant in real galaxies. The Brownian velocity of single black holes is found
in  -body integrations to be [114]
-body integrations to be [114]
where  is the 1D, mean square stellar velocity within a region
is the 1D, mean square stellar velocity within a region  around the black hole (and
includes the influence of the black hole on the stellar motions), and
around the black hole (and
includes the influence of the black hole on the stellar motions), and  is the stellar mass. In
the case of the Milky Way black hole, Equation (42) implies
is the stellar mass. In
the case of the Milky Way black hole, Equation (42) implies  (assuming
(assuming
 ) and an rms displacement of
) and an rms displacement of  . Brownian motion of a massive binary
is larger than that of a single black hole, but only by a modest factor [133
. Brownian motion of a massive binary
is larger than that of a single black hole, but only by a modest factor [133 , 150
, 150 , 128]. The
rms displacement of a binary from its otherwise central location would therefore be very small
in a real galaxy, probably even less than the separation between the two components of the
binary.
The goal of
, 128]. The
rms displacement of a binary from its otherwise central location would therefore be very small
in a real galaxy, probably even less than the separation between the two components of the
binary.
The goal of  -body studies is to simulate binary evolution in galaxies with realistic density
profiles, and with large enough particle numbers that re-population of the binary’s loss cone takes
place diffusively, as in real galaxies. Two avenues are open for making further progress in this
area.
-body studies is to simulate binary evolution in galaxies with realistic density
profiles, and with large enough particle numbers that re-population of the binary’s loss cone takes
place diffusively, as in real galaxies. Two avenues are open for making further progress in this
area.
- One could combine a Monte-Carlo treatment of stellar encounters [57, 58] with a lookup table,
derived from scattering experiments, of energy and angular momentum changes experienced
during close passages of stars to the binary [178, 133]. Such a hybrid algorithm would allow
one to adjust the degree of collisionality at will and record the effects on both the binary’s
evolution, and the influence of the binary on the stellar distribution. This approach would be
difficult to generalize to non-spherical geometries however.
- A straightforward
 -body approach is also feasible, but particle numbers in excess of
-body approach is also feasible, but particle numbers in excess of
 are required [152]. Such large particle numbers are just now becoming feasible for
direct-summation
are required [152]. Such large particle numbers are just now becoming feasible for
direct-summation  -body codes, by combining the GRAPE accelerator boards [127] with
a parallel architecture [33]. Indeed just such an approach was used for the integrations of
Figure 9, although the galaxy models in that study were rather unphysical.
-body codes, by combining the GRAPE accelerator boards [127] with
a parallel architecture [33]. Indeed just such an approach was used for the integrations of
Figure 9, although the galaxy models in that study were rather unphysical.
Figure 10 shows a promising early step in this direction. The initial galaxy models had  density cusps; integrations were carried out on a GRAPE-6 computer, limiting the total particle number
to
density cusps; integrations were carried out on a GRAPE-6 computer, limiting the total particle number
to 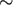 256 K, but the motion of the black hole binary (of mass
256 K, but the motion of the black hole binary (of mass 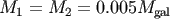 )
and nearby stars was carried out using the Mikkola-Aarseth chain regularization algorithm
[145, 146, 3]. Because of the models’ higher central density and limited particle numbers, the binary’s
loss cone was only partially empty,
)
and nearby stars was carried out using the Mikkola-Aarseth chain regularization algorithm
[145, 146, 3]. Because of the models’ higher central density and limited particle numbers, the binary’s
loss cone was only partially empty,  , and the
, and the  -dependence of the hardening rate
was shallower than expected in real galaxies,
-dependence of the hardening rate
was shallower than expected in real galaxies,  . Figure 10 (a) shows that
the “damage” inflicted by the binary on the nucleus is not strongly dependent on
. Figure 10 (a) shows that
the “damage” inflicted by the binary on the nucleus is not strongly dependent on  , as
expected (cf. Equation 18). This is an encouraging result since it implies that one can hope to
learn something definite about pre-existing binaries by comparing
, as
expected (cf. Equation 18). This is an encouraging result since it implies that one can hope to
learn something definite about pre-existing binaries by comparing  -body simulations with
observations of the centers of current-day galaxies (Section 7). On the other hand, Figure 10
(b) suggests that the evolution of the binary’s eccentricity is strongly
-body simulations with
observations of the centers of current-day galaxies (Section 7). On the other hand, Figure 10
(b) suggests that the evolution of the binary’s eccentricity is strongly  -dependent. This
may explain the rather disparate results on eccentricity evolution in past
-dependent. This
may explain the rather disparate results on eccentricity evolution in past  -body studies
[150
-body studies
[150 , 86, 2].
, 86, 2].
Much progress on this problem is expected in the next few years.
![]() -body studies are likely to give misleading results. This
follows from the result (Section 4.3) that time scales for two-body scattering of stars into the binary’s loss
cone are of order
-body studies are likely to give misleading results. This
follows from the result (Section 4.3) that time scales for two-body scattering of stars into the binary’s loss
cone are of order ![]() or somewhat longer in real galaxies. In
or somewhat longer in real galaxies. In ![]() -body simulations, relaxation times
are shorter by factors of
-body simulations, relaxation times
are shorter by factors of ![]() than in real galaxies, hence the long-term evolution of the binary is
likely to be dominated by spurious loss cone refilling, wandering of the binary, and other noise-driven
effects.
than in real galaxies, hence the long-term evolution of the binary is
likely to be dominated by spurious loss cone refilling, wandering of the binary, and other noise-driven
effects.
![]() -body studies are most useful at characterizing the early stages of binary formation and decay, or
simulating the disruptive tidal effects of a SBH on the nucleus of an infalling galaxy. Due to algorithmic
limitations - primarily the difficulty of integrating galaxy models with high central concentrations - most
such studies [35, 75, 126, 125, 158, 157, 86
-body studies are most useful at characterizing the early stages of binary formation and decay, or
simulating the disruptive tidal effects of a SBH on the nucleus of an infalling galaxy. Due to algorithmic
limitations - primarily the difficulty of integrating galaxy models with high central concentrations - most
such studies [35, 75, 126, 125, 158, 157, 86![]() , 25
, 25![]() , 128
, 128![]() ] have been based on galaxy models with
unrealistically large cores.
] have been based on galaxy models with
unrealistically large cores.
![]() is from the first [136
is from the first [136![]() ]
] ![]() -body simulation of galaxy mergers in which the pre-merger galaxies
contained power-law nuclear cusps as well as massive particles representing the SBHs. These simulations
were run using GADGET [202], a tree code with inter-particle softening, and were not able to accurately follow
the formation and decay of the massive binary. The SBH in the larger galaxy was found to tidally disrupt
the steep cusp in the infalling galaxy, producing a remnant with only slightly higher central density than
that of the giant galaxy initially. This result helps to explain the absence of dense cusps in bright galaxies
[55], and suggests that the central structure of galaxies can only be understood by taking into account the
destructive influence of SBHs on the stellar distribution during mergers. Additional results, using a
similar
-body simulation of galaxy mergers in which the pre-merger galaxies
contained power-law nuclear cusps as well as massive particles representing the SBHs. These simulations
were run using GADGET [202], a tree code with inter-particle softening, and were not able to accurately follow
the formation and decay of the massive binary. The SBH in the larger galaxy was found to tidally disrupt
the steep cusp in the infalling galaxy, producing a remnant with only slightly higher central density than
that of the giant galaxy initially. This result helps to explain the absence of dense cusps in bright galaxies
[55], and suggests that the central structure of galaxies can only be understood by taking into account the
destructive influence of SBHs on the stellar distribution during mergers. Additional results, using a
similar ![]() -body code and a variety of mass ratios for the merging galaxies, were reported in
[141].
-body code and a variety of mass ratios for the merging galaxies, were reported in
[141].
![]() were identical to those
adopted in two other
were identical to those
adopted in two other ![]() -body studies based on a more approximate
-body studies based on a more approximate ![]() -body code [178
-body code [178![]() , 25].
Contrary to Figure 9
, 25].
Contrary to Figure 9![]() , Chatterjee, Hernquist & Loeb (2003) found that the binary hardening
rate “saturated” at values of
, Chatterjee, Hernquist & Loeb (2003) found that the binary hardening
rate “saturated” at values of ![]() , remaining constant up to
, remaining constant up to ![]() . They
speculated that this was due to a kind of Brownian-motion-mediated feedback, in which the
binary maintains a constant supply rate by modulating the local density of stars. However
no supporting evidence for this model was presented; for instance, it was not demonstrated
that the central density was actually regulated by the binary, or that the amplitude of the
Brownian wandering increased with
. They
speculated that this was due to a kind of Brownian-motion-mediated feedback, in which the
binary maintains a constant supply rate by modulating the local density of stars. However
no supporting evidence for this model was presented; for instance, it was not demonstrated
that the central density was actually regulated by the binary, or that the amplitude of the
Brownian wandering increased with ![]() in the manner postulated. Furthermore these authors
provided no plots showing the claimed
in the manner postulated. Furthermore these authors
provided no plots showing the claimed ![]() -dependence of the hardening rate. Chatterjee et al.’s
conclusion, that “a substantial fraction of all massive binaries in galaxies can coalesce within
a Hubble time”, is not substantiated by the more accurate
-dependence of the hardening rate. Chatterjee et al.’s
conclusion, that “a substantial fraction of all massive binaries in galaxies can coalesce within
a Hubble time”, is not substantiated by the more accurate ![]() -body simulations shown in
Figure 9
-body simulations shown in
Figure 9![]() .
.
![]() -body simulations [152
-body simulations [152![]() ], it
is doubtful that the effect is significant in real galaxies. The Brownian velocity of single black holes is found
in
], it
is doubtful that the effect is significant in real galaxies. The Brownian velocity of single black holes is found
in ![]() -body integrations to be [114]
-body integrations to be [114] ![]() shows a promising early step in this direction. The initial galaxy models had
shows a promising early step in this direction. The initial galaxy models had ![]() density cusps; integrations were carried out on a GRAPE-6 computer, limiting the total particle number
to
density cusps; integrations were carried out on a GRAPE-6 computer, limiting the total particle number
to ![]() 256 K, but the motion of the black hole binary (of mass
256 K, but the motion of the black hole binary (of mass ![]() )
and nearby stars was carried out using the Mikkola-Aarseth chain regularization algorithm
[145, 146, 3]. Because of the models’ higher central density and limited particle numbers, the binary’s
loss cone was only partially empty,
)
and nearby stars was carried out using the Mikkola-Aarseth chain regularization algorithm
[145, 146, 3]. Because of the models’ higher central density and limited particle numbers, the binary’s
loss cone was only partially empty, ![]() , and the
, and the ![]() -dependence of the hardening rate
was shallower than expected in real galaxies,
-dependence of the hardening rate
was shallower than expected in real galaxies, ![]() . Figure 10
. Figure 10![]() (a) shows that
the “damage” inflicted by the binary on the nucleus is not strongly dependent on
(a) shows that
the “damage” inflicted by the binary on the nucleus is not strongly dependent on ![]() , as
expected (cf. Equation 18
, as
expected (cf. Equation 18![]() ). This is an encouraging result since it implies that one can hope to
learn something definite about pre-existing binaries by comparing
). This is an encouraging result since it implies that one can hope to
learn something definite about pre-existing binaries by comparing ![]() -body simulations with
observations of the centers of current-day galaxies (Section 7). On the other hand, Figure 10
-body simulations with
observations of the centers of current-day galaxies (Section 7). On the other hand, Figure 10![]() (b) suggests that the evolution of the binary’s eccentricity is strongly
(b) suggests that the evolution of the binary’s eccentricity is strongly ![]() -dependent. This
may explain the rather disparate results on eccentricity evolution in past
-dependent. This
may explain the rather disparate results on eccentricity evolution in past ![]() -body studies
[150
-body studies
[150![]() , 86, 2].
, 86, 2].