4.3 Collisional loss-cone replenishment
A binary black hole depletes its loss cone very quickly since stars within the loss cone need
only a few close encounters with the binary to be ejected. Whether the binary can continue to
exchange energy with stars depends on the efficiency with which stars are re-supplied to the loss
cone.
The most commonly invoked mechanism for loss cone re-filling is two-body scattering of stars. A small
angular momentum perturbation, for instance from a passing star, can deflect a star with  into the
loss cone. This process has been studied in detail in the context of scattering of stars into the tidal
disruption sphere of a single black hole [56
into the
loss cone. This process has been studied in detail in the context of scattering of stars into the tidal
disruption sphere of a single black hole [56 , 119, 27]. The basic equations are similar in the case of
scattering into a binary SBH, except that the critical angular momentum increases by a factor
, 119, 27]. The basic equations are similar in the case of
scattering into a binary SBH, except that the critical angular momentum increases by a factor 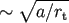 ,
where
,
where  is the tidal disruption radius. (Other differences are discussed below.) If the binary parameters
are assumed fixed, a steady-state flow of stars into the loss cone will be achieved on roughly a
two-body relaxation time scale
is the tidal disruption radius. (Other differences are discussed below.) If the binary parameters
are assumed fixed, a steady-state flow of stars into the loss cone will be achieved on roughly a
two-body relaxation time scale  , and the distribution function near
, and the distribution function near  will have the form
will have the form
where  is a scaled angular momentum variable,
is a scaled angular momentum variable,  ,
,  is the angular
momentum of a circular orbit of energy
is the angular
momentum of a circular orbit of energy  , and
, and  is the distribution function far from the loss
cone, assumed to be isotropic. The mass flow into the central object is
is the distribution function far from the loss
cone, assumed to be isotropic. The mass flow into the central object is  , where
The quantity in brackets is the orbit-averaged diffusion coefficient in
, where
The quantity in brackets is the orbit-averaged diffusion coefficient in  .
.
A crude estimate of the collisional re-supply rate is given by
[56], where  is the mass in stars within radius
is the mass in stars within radius  and
and  is the critical radius at which stars
scatter into the loss cone in a single orbital period; beyond
is the critical radius at which stars
scatter into the loss cone in a single orbital period; beyond  , the diffusion rate drops rapidly with
radius. Estimates based on simple galaxy models give
, the diffusion rate drops rapidly with
radius. Estimates based on simple galaxy models give  . To get an idea of the scattering
rate, we consider the nucleus of the Milky Way. Equation (4) gives
. To get an idea of the scattering
rate, we consider the nucleus of the Milky Way. Equation (4) gives  . Assuming
. Assuming
 ,
,  and
and 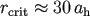 gives
gives  . The mass within this radius is
. The mass within this radius is
 [66
[66 ] and the relaxation time at this radius, assuming stars of a solar mass, is
] and the relaxation time at this radius, assuming stars of a solar mass, is
 . The scattered mass over
. The scattered mass over  is then
is then  . This is comparable to the
mass of the Milky Way SMBH,
. This is comparable to the
mass of the Milky Way SMBH,  [195], but the scattering rate would drop as
the binary shrinks, suggesting that scattered stars would contribute only modestly to refilling
of the loss cone. In more massive galaxies, the nuclear density is lower, relaxation times are
longer, and collisional refilling would be even less important. A more detailed calculation of the
collisional refilling rates in real galaxies [228
[195], but the scattering rate would drop as
the binary shrinks, suggesting that scattered stars would contribute only modestly to refilling
of the loss cone. In more massive galaxies, the nuclear density is lower, relaxation times are
longer, and collisional refilling would be even less important. A more detailed calculation of the
collisional refilling rates in real galaxies [228 ] concludes that few if any binary SBHs could reach
coalescence via this mechanism. The author took the presently observed luminosity profiles of
galaxies as initial conditions. The stellar density profiles must have been steeper before the
binary SBH formed [150
] concludes that few if any binary SBHs could reach
coalescence via this mechanism. The author took the presently observed luminosity profiles of
galaxies as initial conditions. The stellar density profiles must have been steeper before the
binary SBH formed [150 ], leading to substantially more rapid decay early in the life of the
binary.
], leading to substantially more rapid decay early in the life of the
binary.
Another criticism of standard loss cone theory is its assumption of a quasi-steady-state distribution of
stars in phase space near  [152
[152 ]. This assumption is appropriate at the center of a globular cluster,
where relaxation times are much shorter than the age of the universe, but is less appropriate for a galactic
nucleus, where relaxation times almost always greatly exceed a Hubble time [44
]. This assumption is appropriate at the center of a globular cluster,
where relaxation times are much shorter than the age of the universe, but is less appropriate for a galactic
nucleus, where relaxation times almost always greatly exceed a Hubble time [44 ]. (The exceptions are
the nuclei of small dense systems like the bulge of the Milky Way.) The distribution function
]. (The exceptions are
the nuclei of small dense systems like the bulge of the Milky Way.) The distribution function
 immediately following the formation of a hard binary is approximately a step function,
immediately following the formation of a hard binary is approximately a step function,
much steeper than the  dependence in a collisonally relaxed nucleus (Equation 31). Since the
transport rate in phase space is proportional to the gradient of
dependence in a collisonally relaxed nucleus (Equation 31). Since the
transport rate in phase space is proportional to the gradient of  with respect to
with respect to  , steep gradients
imply an enhanced flux into the loss cone. Figure 6 shows the evolution of
, steep gradients
imply an enhanced flux into the loss cone. Figure 6 shows the evolution of 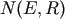 at a single
at a single 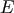 assuming that the loss cone is empty initially within some
assuming that the loss cone is empty initially within some  and that
and that  is a
constant function of
is a
constant function of 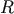 outside of
outside of  . (The loss cone boundary is assumed static; in reality it would
shrink with the binary.) Also shown is the collisionally-relaxed solution of Equation (31). The phase-space
gradients decay rapidly at first and then more gradually as they approach the steady-state
solution. The total mass consumed by the binary, shown in the lower panel of Figure 6, is
substantially greater than would be computed from the steady-state theory, implying greater cusp
destruction and more rapid decay of the binary. This time-dependent loss cone refilling might be
particularly effective in a nucleus that continues to experience mergers or accretion events, in such
a way that the loss cone repeatedly returns to an unrelaxed state with its associated steep
gradients.
There are other differences between loss cones around single and binary SBHs. A star that interacts with
a massive binary generally remains inside the galaxy and is available for further interactions. In principle, a
single star can interact many times with the binary before being ejected from the galaxy or falling
outside the loss cone; each interaction takes additional energy from the binary and hastens its
decay. Consider a simple model in which a group of
. (The loss cone boundary is assumed static; in reality it would
shrink with the binary.) Also shown is the collisionally-relaxed solution of Equation (31). The phase-space
gradients decay rapidly at first and then more gradually as they approach the steady-state
solution. The total mass consumed by the binary, shown in the lower panel of Figure 6, is
substantially greater than would be computed from the steady-state theory, implying greater cusp
destruction and more rapid decay of the binary. This time-dependent loss cone refilling might be
particularly effective in a nucleus that continues to experience mergers or accretion events, in such
a way that the loss cone repeatedly returns to an unrelaxed state with its associated steep
gradients.
There are other differences between loss cones around single and binary SBHs. A star that interacts with
a massive binary generally remains inside the galaxy and is available for further interactions. In principle, a
single star can interact many times with the binary before being ejected from the galaxy or falling
outside the loss cone; each interaction takes additional energy from the binary and hastens its
decay. Consider a simple model in which a group of  stars in a spherical galaxy interact
with the binary and receive a mean energy increment of
stars in a spherical galaxy interact
with the binary and receive a mean energy increment of  . Let the original energy of
the stars be
. Let the original energy of
the stars be 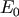 . Averaged over a single orbital period
. Averaged over a single orbital period  , the binary hardens at a rate
In subsequent interactions, the number of stars that remain inside the loss cone scales as
, the binary hardens at a rate
In subsequent interactions, the number of stars that remain inside the loss cone scales as  while
the ejection energy scales as
while
the ejection energy scales as  . Hence
. Hence  . Assuming the singular isothermal
sphere potential for the galaxy, one finds
[152
. Assuming the singular isothermal
sphere potential for the galaxy, one finds
[152 ]. Hence the binary’s binding energy increases as the logarithm of the time, even after all the stars in
the loss cone have interacted at least once with the binary. Re-ejection would occur differently in
nonspherical galaxies where angular momentum is not conserved and ejected stars could miss the binary on
their second passage. However there will generally exist a subset of orbits defined by a maximum
pericenter distance
]. Hence the binary’s binding energy increases as the logarithm of the time, even after all the stars in
the loss cone have interacted at least once with the binary. Re-ejection would occur differently in
nonspherical galaxies where angular momentum is not conserved and ejected stars could miss the binary on
their second passage. However there will generally exist a subset of orbits defined by a maximum
pericenter distance  and stars scattered onto such orbits can continue to interact with the
binary.
and stars scattered onto such orbits can continue to interact with the
binary.
As these arguments suggest, the long-term evolution of a binary SBH due to interactions with stars may
be very different in different environments. (We stress that the presence of gas may substantially alter this
picture; cf. Section 8.) There are three characteristic regimes [152 ].
].
- Collisional. The relaxation time
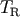 is shorter than the lifetime of the system and the
phase-space gradients at the edge of the loss cone are given by steady-state solutions to the
Fokker-Planck equation. The densest galactic nuclei may be in this regime. Resupply of the
loss cone takes place on the time scale associated with scattering of stars onto eccentric orbits.
The decay time of a binary SBH scales as
is shorter than the lifetime of the system and the
phase-space gradients at the edge of the loss cone are given by steady-state solutions to the
Fokker-Planck equation. The densest galactic nuclei may be in this regime. Resupply of the
loss cone takes place on the time scale associated with scattering of stars onto eccentric orbits.
The decay time of a binary SBH scales as  with
with  the number of stars.
In the densest galactic nuclei, collisional loss cone refilling may just be able to drive a binary
SBH to coalescence in a Hubble time. For sufficiently small
the number of stars.
In the densest galactic nuclei, collisional loss cone refilling may just be able to drive a binary
SBH to coalescence in a Hubble time. For sufficiently small  , scattering refills the loss cone
in less than an orbital period (“full loss cone”) and the decay follows
, scattering refills the loss cone
in less than an orbital period (“full loss cone”) and the decay follows  .
.  -body
studies are typically in this regime, as discussed below.
-body
studies are typically in this regime, as discussed below.
- Collisionless. The relaxation time is longer than the system lifetime and gravitational
encounters between stars can be ignored. The low-density nuclei of bright elliptical galaxies are
in this regime. The binary SBH quickly interacts with stars whose pericenters lie within its
sphere of influence; in a low-density (spherical or axisymmetric) nucleus, the associated mass is
less than that of the binary and the decay tends to stall at a separation too large for gravitational
wave emission to be effective. However evolution can continue due to re-ejection of stars that
lie within the binary’s loss cone but have not yet escaped from the system. In the spherical
geometry, re-ejection implies
 , leading to a logarithmic dependence of
binary hardness on time. Re-ejection in galactic nuclei may contribute a factor of
, leading to a logarithmic dependence of
binary hardness on time. Re-ejection in galactic nuclei may contribute a factor of  a few to
the change in
a few to
the change in  over a Hubble time.
over a Hubble time.
- Intermediate. The relaxation time is of order the age of the system or somewhat longer. While
gravitational encounters contribute to the re-population of the loss cone, not enough time has
elapsed for the phase space distribution to have reached a collisional steady state. Most galactic
nuclei are probably in this regime. The flux of stars into the loss cone can be substantially
higher than predicted by the steady-state theory, due to strong gradients in the phase space
density near the loss cone boundary produced when the binary SBH initially formed. This
transitory enhancement would be most important in a nucleus that continues to experience
mergers or infall, in such a way that the loss cone repeatedly returns to an unrelaxed state with
its associated steep gradients.
Table 2 summarizes the different regimes. The evolution of a real binary SBH may reflect a combination
of these and other mechanisms, such as interaction with gas. There is a close parallel between the final
parsec problem and the problem of quasar fueling: Both require that of order  be
supplied to the inner parsec of a galaxy in a time shorter than the age of the universe. Nature
clearly accomplishes this in the case of quasars, probably through gas flows driven by torques
from stellar bars. The same inflow of gas could contribute to the decay of a binary SBH in a
number of ways: by leading to the renewed formation of stars which subsequently interact with
the binary; by inducing torques which extract angular momentum from the binary; through
accretion, increasing the masses of one or both of the SBHs and reducing their separation;
etc.
be
supplied to the inner parsec of a galaxy in a time shorter than the age of the universe. Nature
clearly accomplishes this in the case of quasars, probably through gas flows driven by torques
from stellar bars. The same inflow of gas could contribute to the decay of a binary SBH in a
number of ways: by leading to the renewed formation of stars which subsequently interact with
the binary; by inducing torques which extract angular momentum from the binary; through
accretion, increasing the masses of one or both of the SBHs and reducing their separation;
etc.
|
|
| Form of Decay |
Regime |
|
|
 |
Collisionless |
 |
Collisional (diffusion) |
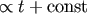 |
Collisional (full loss cone) |
 |
Re-ejection |
|
|
| Table 2: |
Physical Regimes for Long-Term Decay of
Massive Black Hole Binaries |
|
| |
| |
| |
| |
|
![]() into the
loss cone. This process has been studied in detail in the context of scattering of stars into the tidal
disruption sphere of a single black hole [56
into the
loss cone. This process has been studied in detail in the context of scattering of stars into the tidal
disruption sphere of a single black hole [56![]() , 119, 27]. The basic equations are similar in the case of
scattering into a binary SBH, except that the critical angular momentum increases by a factor
, 119, 27]. The basic equations are similar in the case of
scattering into a binary SBH, except that the critical angular momentum increases by a factor ![]() ,
where
,
where ![]() is the tidal disruption radius. (Other differences are discussed below.) If the binary parameters
are assumed fixed, a steady-state flow of stars into the loss cone will be achieved on roughly a
two-body relaxation time scale
is the tidal disruption radius. (Other differences are discussed below.) If the binary parameters
are assumed fixed, a steady-state flow of stars into the loss cone will be achieved on roughly a
two-body relaxation time scale ![]() , and the distribution function near
, and the distribution function near ![]() will have the form
will have the form
![]() [152
[152![]() ]. This assumption is appropriate at the center of a globular cluster,
where relaxation times are much shorter than the age of the universe, but is less appropriate for a galactic
nucleus, where relaxation times almost always greatly exceed a Hubble time [44
]. This assumption is appropriate at the center of a globular cluster,
where relaxation times are much shorter than the age of the universe, but is less appropriate for a galactic
nucleus, where relaxation times almost always greatly exceed a Hubble time [44![]() ]. (The exceptions are
the nuclei of small dense systems like the bulge of the Milky Way.) The distribution function
]. (The exceptions are
the nuclei of small dense systems like the bulge of the Milky Way.) The distribution function
![]() immediately following the formation of a hard binary is approximately a step function,
immediately following the formation of a hard binary is approximately a step function,
![]() ].
].
![]() be
supplied to the inner parsec of a galaxy in a time shorter than the age of the universe. Nature
clearly accomplishes this in the case of quasars, probably through gas flows driven by torques
from stellar bars. The same inflow of gas could contribute to the decay of a binary SBH in a
number of ways: by leading to the renewed formation of stars which subsequently interact with
the binary; by inducing torques which extract angular momentum from the binary; through
accretion, increasing the masses of one or both of the SBHs and reducing their separation;
etc.
be
supplied to the inner parsec of a galaxy in a time shorter than the age of the universe. Nature
clearly accomplishes this in the case of quasars, probably through gas flows driven by torques
from stellar bars. The same inflow of gas could contribute to the decay of a binary SBH in a
number of ways: by leading to the renewed formation of stars which subsequently interact with
the binary; by inducing torques which extract angular momentum from the binary; through
accretion, increasing the masses of one or both of the SBHs and reducing their separation;
etc.