3.3 Chaotic scalar field dynamics 

Many studies of cosmological models generally reduce complex physical systems to simplified or even analytically integrable systems. In sufficiently simple models the dynamical behavior (or fate) of the Universe can be predicted from a given set of initial conditions. However, the Universe is composed of many different nonlinear interacting fields including the inflaton field which can exhibit complex chaotic behavior. For example, Cornish and Levin [57] consider a homogenous isotropic closed FLRW model with various conformal and minimally coupled scalar fields (see § 6.3.2). They find that even these relatively simple models exhibit chaotic transients in their early pre-inflationary evolution. This behavior in exiting the Planck era is characterized by fractal basins of attraction, with attractor states being to (1) inflate forever, (2) inflate over a short period of time then collapse, or (3) collapse without inflating. Monerat et al. [98] investigated the dynamics of the pre-inflationary phase of the Universe and its exit to inflation in a closed FLRW model with radiation and a minimally coupled scalar field. They observe complex behavior associated with saddle-type critical points in phase space that give rise to deSitter attractors with multiple chaotic exits to inflation that depend on the structure of the scalar field potential. These results suggest that distinctions between exits to inflation may be manifested in the process of reheating and as a selected spectrum of inhomogeneous perturbations influenced by resonance mechanisms in curvature oscillations. This could possibly lead to fractal patterns in the density spectrum, gravitational waves, CMBR field, or galaxy distribution that depend on specific details including the number of fields, the nature of the fields, and their interaction potentials.

Chaotic behavior can also be found in more general applications of scalar field dynamics. Anninos et al. [18] investigated the nonlinear behavior of colliding kink-antikink solitons or domain walls described by a single real scalar field with self-interaction potential 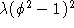. Domain walls can form as topological defects during the spontaneous symmetry breaking period associated with phase transitions, and can seed density fluctuations in the large scale structure. For collisional time scales much smaller than the cosmological expansion, they find that whether a kink-antikink collision results in a bound state or a two-soliton solution depends on a fractal structure observed in the impact velocity parameter space. The fractal structure arises from a resonance condition associated with energy exchanges between translational modes and internal shape-mode oscillations. The impact parameter space is a complex self-similar fractal composed of sequences of different n-bounce (the number of bounces or oscillations in the transient semi-coherent state) reflection windows separated by regions of oscillating bion states (see Figure 3). They compute the Lyapunov exponents for parameters in which a bound state forms to demonstrate the chaotic nature of the bion oscillations.

  

Figure 3: Fractal structure of the transition between reflected and captured states for colliding kink-antikink solitons in the parameter space of impact velocity for a 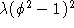scalar field potential. The top image (a) shows the 2-bounce windows in dark with the rightmost region (v/c > 0.25) representing the single-bounce regime above which no captured state exists, and the leftmost white region (v/c < 0.19) representing the captured state below which no reflection windows exist. Between these two marker velocities, there are 2-bounce reflection states of decreasing widths separated by regions of bion formation. Zooming in on the domain outlined by the dashed box, a self-similar structure is apparent in the middle image (b), where now the dark regions represent 3-bounce windows of decreasing widths. Zooming in once again on the boundaries of these 3-bounce windows, a similar structure is found as shown in the bottom image (c) but with 4-bounce reflection windows. This pattern of self-similarity with n-bounce windows is observed at all scales investigated numerically.

Computational Cosmology: from the Early Universe to the Large Scale Structure Peter Anninos http://www.livingreviews.org/lrr-2001-2 © Max-Planck-Gesellschaft. ISSN 1433-8351 Problems/Comments to livrev@aei-potsdam.mpg.de