3.2 Inflation 

The inflation paradigm is frequently invoked to explain the flatness ( 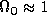in the context of the FLRW model) and nearly isotropic nature of the Universe at large scales, attributing them to an era of exponential expansion at about after the Big Bang. This expansion acts as a strong dampening mechanism to random curvature or density fluctuations, and may be a generic attractor in the space of initial conditions. An essential component needed to trigger this inflationary phase is a scalar or inflaton field representing spin zero particles. The vacuum energy of the field acts as an effective cosmological constant that regulates GUT symmetry breaking, particle creation, and the reheating of the Universe through an interaction potential derived from the form of symmetry breaking that occurs as the temperature of the Universe decreases. Early analytic studies focused on simplified models, treating the interaction potential as flat near its local maximum where the field does not evolve significantly and where the formal analogy to an effective cosmological constant approximation is more precise. However, to properly account for the complexity of inflaton fields, the full dynamical equations (see § 6.3.2) must be considered together with consistent curvature, matter and other scalar field couplings. Also, many different theories of inflation and vacuum potentials have been proposed (see, for example, a recent review by Lyth and Riotto [91] and an introductory article by Liddle [90]), and it is not likely that simplified models can elucidate the full nonlinear complexity of scalar fields (see § 3.3) nor the generic nature of inflation.

In order to study whether inflation can occur for arbitrary anisotropic and inhomogeneous data, many numerical simulations have been carried out with different symmetries, matter types and perturbations. A sample of such calculations is described in the following paragraphs.

3.2.1 Plane symmetry 

Kurki-Suonio et al. [85] extended the planar cosmology code of Centrella and Wilson [54, 55] (see § 3.6) to include a scalar field and simulate the onset of inflation in the early Universe with an inhomogeneous Higgs field and a perfect fluid with a radiation equation of state , where p is the pressure and is the energy density. Their results suggest that whether inflation occurs or not can be sensitive to the shape of the potential . In particular, if the shape is flat enough and satisfies the slow-roll conditions (essentially upper bounds on and  [84] near the false vacuum ), even large initial fluctuations of the Higgs field do not prevent inflation. They considered two different forms of the potential: a Coleman-Weinberg type with interaction strength

which is very flat close to the false vacuum and does inflate; and a rounder `` '' type

which, for their parameter combinations, does not.

3.2.2 Spherical symmetry 

Goldwirth and Piran [71] studied the onset of inflation with inhomogeneous initial conditions for closed, spherically symmetric spacetimes containing a massive scalar field and radiation field sources (described by a massless scalar field). In all the cases they considered, the radiation field damps quickly and only an inhomogeneous massive scalar field remains to inflate the Universe. They find that small inhomogeneities tend to reduce the amount of inflation and large initial inhomogeneities can even suppress the onset of inflation. Their calculations indicate that the scalar field must have ``suitable'' initial values over a domain of several horizon lengths in order for inflation to begin.

3.2.3 Bianchi V 

Anninos et al. [12] investigated the simplest Bianchi model (type V) background that admits velocities or tilt in order to address the question of how the Universe can choose a uniform reference frame at the exit from inflation, since the de Sitter metric does not have a preferred frame. They find that inflation does not isotropize the Universe in the short wavelength limit. However, if inflation persists, the wave behavior eventually freezes in and all velocities go to zero at least as rapidly as , where is the relativistic tilt angle (a measure of velocity), and R is a typical scale associated with the radius of the Universe. Their results indicate that the velocities eventually go to zero as inflation carries all spatial variations outside the horizon, and that the answer to the posed question is that memory is retained and the Universe is never really de Sitter.

3.2.4 Gravity waves + cosmological constant 

In addition to the inflaton field, one can consider other sources of inhomogeneity, such as gravitational waves. Although linear waves in de Sitter space will decay exponentially and disappear, it is unclear what will happen if strong waves exist. Shinkai & Maeda [116] investigated the cosmic no-hair conjecture with gravitational waves and a cosmological constant ( ) in 1D plane symmetric vacuum spacetimes, setting up Gaussian pulse wave data with amplitudes and widths 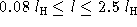, where I is the invariant constructed from the 3-Riemann tensor and is the horizon scale. They also considered colliding plane waves with amplitudes and widths . They find that for any large amplitude or small width inhomogeneity in their parameter sets, the nonlinearity of gravity has little effect and the spacetime always evolves towards de Sitter.

3.2.5 3D inhomogeneous spacetimes 

The previous paragraphs discussed results from highly symmetric spacetimes, but the possibility of inflation remains to be established for more general inhomogeneous and nonperturbative data. In an effort to address this issue, Kurki-Suonio et al. [86] investigated fully three-dimensional inhomogeneous spacetimes with a chaotic inflationary potential . They considered basically two types of runs: small and large scale. In the small scale run, the grid length was initially set equal to the Hubble length so the inhomogeneities are well inside the horizon and the dynamical time scale is shorter than the expansion or Hubble time. As a result, the perturbations oscillate and damp, while the field evolves and the spacetime inflates. In the large scale run, the inhomogeneities are outside the horizon and they do not oscillate. They maintain their shape without damping and, because larger values of lead to faster expansion, the inhomogeneity in the expansion becomes steeper in time since the regions of large and high inflation stay correlated. Both runs have sufficient inflation to solve the flatness problem.

Computational Cosmology: from the Early Universe to the Large Scale Structure Peter Anninos http://www.livingreviews.org/lrr-2001-2 © Max-Planck-Gesellschaft. ISSN 1433-8351 Problems/Comments to livrev@aei-potsdam.mpg.de