5.3 Bursts
Bursts are time-localized signals in the data set. Matched filtering with assumed waveforms involves
varying several parameters, including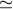 
, in the three-pulse response. Burst searches are helped by the
very diagnostic three-pulse response (integral of signal response must be zero; location and amplitude ratios
of the “pulses” must be consistent with 
.) Matched filter outputs have a “signal part” (integral of
the matching function with the signal) and a “noise part” (integral of the matching function
with the noise). The variance of the matched-filter’s noise-only output changes if the noise is
non-stationary. If not accounted for this can result in distorted pdfs of matched filter outputs and
(superficially significant) tails of the distribution of matched filter outputs, even in the absence
of a signal. To allow for this [60
] the data can be divided into intervals over which the noise
appears stationary. A model of the noise spectrum over each interval is used, along with the
assumed signal waveform, to compute the matching function. This matching function is then
used for that interval only. Simulation of the matched filter against synthetic noise having the
same spectrum and data gap structure of the interval being analyzed is used to estimate the
variance of the noise-only matched filter output. Then the actual matched filter outputs can be
normalized by the estimated noise-only variance to express outputs in terms of SNRs. This
allows the outputs of the matched filter to be compared consistently across a data set where
the noise statistics are changing. Multi-spacecraft coincidences can be used to reduce further
false-alarms [29, 106, 60, 13].
Related to burst processing are “template independent” methods for identifying data intervals for more
detailed study. Wavelet transforms of the data on a pass-by-pass basis have been sometimes useful in finding
time-localized intervals formally contributing anomalously large variance. These are then typically checked
to see if there are corresponding features within 
T2. Examination of the time series reconstructed from
some small fraction (
10%) of the largest amplitude wavelets (or systematically from the wavelets in
selected subbands only) have also been useful [11].
