Burst waves

6.3 Burst waves

The first systematic search for burst radiation was done by filtering the data to de-emphasize the dominant noise (plasma noise) relative to components of the time series anticorrelated at the two-way light time [57 ]. Analysis of subsequent data sets used matched filtering with assumed waveforms and targeted-sky-directions [7

, 60

, 61

]. The utility of multiple-spacecraft observations for burst searches was discussed by [29

, 106 , 13 ]. Figure 20

is the crudest measure of current-generation (Ka-band, tropospheric corrected) all-sky burst sensitivity. It shows the power spectrum of two-way Doppler divided by the isotropic GW transfer function (see, e.g., [49

, 51

] and Section 5.4) computed as [102 ] $h (f) = [2fSgw ∕R¯ (f)]1∕2 c y2 2$ , where $R¯ (f) 2$ is the sky- and polarization-averaged GW response function [49

, 51

, 19

]. The best sensitivity, h_c 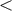$<$ 2 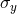$×$ 10^–15, occurs at about 0.3 mHz, set by the minimization of the antenna mechanical noise through its transfer function, the bandwidth, and the average coupling of the GW to the Doppler, $R¯2$ , at this frequency.

Figure 20:

Characteristic all-sky strain sensitivity for a burst wave having a bandwidth comparable to center frequency for the Cassini 2001–2002 data set [19

]. This is the crudest measure of sky-averaged burst sensitivity: the square root of the product of the Doppler spectrum and the Fourier frequency, divided by the sky-averaged GW response (see Section 6.3).

Sensitivity is not uniform over the sky and one can often do much better with knowledge of the direction-of-arrival or the waveform. Figure 21 shows contours of constant matched filter output for a circularly polarized mid-band burst wave using the Cassini solar opposition geometry of November 2003. The red dot shows the right ascension and declination of Cassini as viewed from the earth, the black dots are the positions of members of the Local Group of galaxies (larger dots indicating nearer objects), and “GC” marks the location of the Galactic center. Contour levels are at 1/10 of the maximum, with red contours at 0.9 to 0.5 of the maximum filter output and blue contours at 0.4 to 0.1. The response is zero in the direction and anti-direction of the earth-Cassini vector (see Equation (1 )). The angular response changes for GWs in the long-wavelength limit. Figure 22 similarly shows matched filter signal output contours, but for a burst wave with characteristic duration $>$ T₂. Pilot analyses using simplified waveforms [60 , 11 ] have been done accounting for the local non-stationarity of the noise and varying assumed source position on the sky.

Figure 21:

Contours of constant matched filter output for a wave having $h+ (t) = sin(2πt ⋅ 0.001 Hz)exp (− t∕1000 s)H (t)$ and $h×(t)$ its Hilbert transform, adapted from [61 ]. Cassini November 2003 geometry is assumed (the red dot is the right ascension and declination of Cassini). Black dots are the positions of members of the Local Group of galaxies. “GC” marks the location of the galactic center. Contour levels are at 1/10 of the maximum, with red contours at 0.9 to 0.5 of the maximum signal output and blue contours at 0.4 to 0.1. Doppler response is zero in the direction of Cassini (and its anti-direction).

Waves from coalescing binary sources are intermediate between periodic and burst waves. Expected sensitivity and analysis methods have been treated in detail by Bertotti, Iess, and Vecchio [31 , 117 ]; supermassive black hole coalescences with favorable parameters are visible with Cassini-class sensitivity out to 100s of Mpc. Cassini is also sensitive to $≃ 50M ⊙$ intermediate-mass black holes coalescing with the supermassive black hole at the galactic center [31 ].

Figure 22:

As in Figure 21

but for a wave with $h+ (t) = sin(2πt ⋅ 0.0001 Hz) exp(− t∕10000 s)H (t)$ and $h×(t)$ its Hilbert transform. This model waveform is long compared with T₂.