The model

8.1 The model

In this model the black hole spacetime is described by a spherically symmetric static metric with a line element of the following general form written in advanced time Eddington–Finkelstein coordinates,

where $ψ = ψ (r)$ and $m = m (r)$ , $( ) v = t + r + 2M ln 2rM-− 1$ , and $dΩ2$ is the line element on the two-sphere. Hawking radiation is described by a massless, conformally coupled quantum scalar field $φ$ with the classical action

where $ξ(n) = (n−2)- 4(n−1)$ ( $n$ is the dimension of spacetime), and $R$ is the curvature scalar of the spacetime it lives in.

Let us consider linear perturbations $hμν$ off a background Schwarzschild metric $g(0μ)ν$ ,

with standard line element

We look for this class of perturbed metrics in the form given by Equation (153

) (thus restricting our consideration only to spherically symmetric perturbations),

and

where $ε∕(λM 2) = 13aT 4H$ with $2 a = π30-$ and $λ = 90(84)π2$ , and where $TH$ is the Hawking temperature. This particular parametrization of the perturbation is chosen following York’s notation [297

, 298

, 299

]. Thus the only non-zero components of $hμν$ are

and

So this represents a metric with small static and radial perturbations about a Schwarzschild black hole. The initial quantum state of the scalar field is taken to be the Hartle–Hawking vacuum, which is essentially a thermal state at the Hawking temperature and it represents a black hole in (unstable) thermal equilibrium with its own Hawking radiation. In the far field limit, the gravitational field is described by a linear perturbation of Minkowski spacetime. 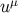In equilibrium the thermal bath can be characterized by a relativistic fluid with a four-velocity (time-like normalized vector field) $uμ$ , and temperature in its own rest frame $−1 β$ .

To facilitate later comparisons with our program we briefly recall York’s work [297 , 298 , 299 ]. (See also the work by Hochberg and Kephart [135 ] for a massless vector field, by Hochberg, Kephart, and York [136 ] for a massless spinor field, and by Anderson, Hiscock, Whitesell, and York [8 ] for a quantized massless scalar field with arbitrary coupling to spacetime curvature.) York considered the semiclassical Einstein equation,

with $G μν ≃ G (0μ)ν + δG μν$ , where $G(μ0ν)$ is the Einstein tensor for the background spacetime. The zeroth order solution gives a background metric in empty space, i.e, the Schwarzschild metric. $δG μν$ is the linear correction to the Einstein tensor in the perturbed metric. The semiclassical Einstein equation in this approximation therefore reduces to

York solved this equation to first order by using the expectation value of the energy-momentum tensor for a conformally coupled scalar field in the Hartle–Hawking vacuum in the unperturbed (Schwarzschild) spacetime on the right-hand side and using Equations (159

) and (160

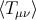) to calculate $δG μν$ on the left-hand side. Unfortunately, no exact analytical expression is available for the $⟨Tμν⟩$ in a Schwarzschild metric with the quantum field in the Hartle–Hawking vacuum that goes on the right-hand side. York therefore uses the approximate expression given by Page [230

] which is known to give excellent agreement with numerical results. Page’s approximate expression for $⟨Tμν⟩$ was constructed using a thermal Feynman Green’s function obtained by a conformal transformation of a WKB approximated Green’s function for an optical Schwarzschild metric. York then solves the semiclassical Einstein equation (162

) self-consistently to obtain the corrections to the background metric induced by the backreaction encoded in the functions $μ(r)$ and $ρ (r)$ . There was no mention of fluctuations or its effects. As we shall see, in the language of Sec. (4), the semiclassical gravity procedure which York followed working at the equation of motion level is equivalent to looking at the noise-averaged backreaction effects.