7.1 The model
In this chaotic inflationary model [199] the inflaton field  of mass
of mass  is described by the following
Lagrangian density:
The conditions for the existence of an inflationary period, which is characterized by an accelerated
cosmological expansion, is that the value of the field over a region with the typical size of the Hubble radius
is higher than the Planck mass
is described by the following
Lagrangian density:
The conditions for the existence of an inflationary period, which is characterized by an accelerated
cosmological expansion, is that the value of the field over a region with the typical size of the Hubble radius
is higher than the Planck mass 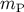 . This is because in order to solve the cosmological horizon and flatness
problem more than 60 e-folds of expansion are needed; to achieve this the scalar field should begin with a
value higher than
. This is because in order to solve the cosmological horizon and flatness
problem more than 60 e-folds of expansion are needed; to achieve this the scalar field should begin with a
value higher than  . The inflaton mass is small: As we will see, the large scale anisotropies measured in
the cosmic background radiation [265
. The inflaton mass is small: As we will see, the large scale anisotropies measured in
the cosmic background radiation [265 ] restrict the inflaton mass to be of the order of
] restrict the inflaton mass to be of the order of  . We will
not discuss the naturalness of this inflationary model and we will simply assume that if one
such region is found (inside a much larger universe) it will inflate to become our observable
universe.
. We will
not discuss the naturalness of this inflationary model and we will simply assume that if one
such region is found (inside a much larger universe) it will inflate to become our observable
universe.
We want to study the metric perturbations produced by the stress-energy tensor fluctuations of the
inflaton field on the homogeneous background of a flat Friedmann–Robertson–Walker model, described by
the cosmological scale factor  , where
, where  is the conformal time, which is driven by the
homogeneous inflaton field
is the conformal time, which is driven by the
homogeneous inflaton field  . Thus we write the inflaton field in the following form:
. Thus we write the inflaton field in the following form:
where  corresponds to a free massive quantum scalar field with zero expectation value on the
homogeneous background metric,
corresponds to a free massive quantum scalar field with zero expectation value on the
homogeneous background metric,  . We will restrict ourselves to scalar-type metric perturbations,
because these are the ones that couple to the inflaton fluctuations in the linear theory. We note that this is
not so if we were to consider inflaton fluctuations beyond the linear approximation; then tensorial and
vectorial metric perturbations would also be driven. The perturbed metric
. We will restrict ourselves to scalar-type metric perturbations,
because these are the ones that couple to the inflaton fluctuations in the linear theory. We note that this is
not so if we were to consider inflaton fluctuations beyond the linear approximation; then tensorial and
vectorial metric perturbations would also be driven. The perturbed metric  can be written
in the longitudinal gauge as
where the scalar metric perturbations
can be written
in the longitudinal gauge as
where the scalar metric perturbations  and
and  correspond to Bardeen’s gauge invariant
variables [12].
correspond to Bardeen’s gauge invariant
variables [12].
![]() , where
, where ![]() is the conformal time, which is driven by the
homogeneous inflaton field
is the conformal time, which is driven by the
homogeneous inflaton field ![]() . Thus we write the inflaton field in the following form:
. Thus we write the inflaton field in the following form: