4.2 Horizon solution in series of hypergeometric functions
As in Section 3, we focus on the ingoing wave function of the radial Teukolsky equation (14). Since the
analysis below is applicable to any spin, 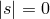 ,
,  ,
,  ,
,  , and
, and  , we do not specify it
except when it is needed. Also, the analysis is not restricted to the case
, we do not specify it
except when it is needed. Also, the analysis is not restricted to the case  unless so
stated explicitly. For general spin weight
unless so
stated explicitly. For general spin weight  , the homogeneous Teukolsky equation is given by
As before, taking account of the symmetry
, the homogeneous Teukolsky equation is given by
As before, taking account of the symmetry  , we may assume
, we may assume 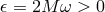 if
necessary.
if
necessary.
The Teukolsky equation has two regular singularities at  , and one irregular singularity at
, and one irregular singularity at
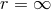 . This implies that it cannot be represented in the form of a single hypergeometric equation.
However, if we focus on the solution near the horizon, it may be approximated by a hypergeometric
equation. This motivates us to consider the solution expressed in terms of a series of hypergeometric
functions.
. This implies that it cannot be represented in the form of a single hypergeometric equation.
However, if we focus on the solution near the horizon, it may be approximated by a hypergeometric
equation. This motivates us to consider the solution expressed in terms of a series of hypergeometric
functions.
We define the independent variable  in place of
in place of  (
( ) as
) as
where
For later convenience, we also introduce  and
and 
 . Taking into account the
structure of the singularities at
. Taking into account the
structure of the singularities at  , we put the ingoing wave Teukolsky function
, we put the ingoing wave Teukolsky function  as
Then the radial Teukolsky equation becomes
where a prime denotes
as
Then the radial Teukolsky equation becomes
where a prime denotes  . The left-hand side of Equation (117) is in the form of a hypergeometric
equation. In the limit
. The left-hand side of Equation (117) is in the form of a hypergeometric
equation. In the limit  , noting Equation (110), we find that a solution that is finite at
, noting Equation (110), we find that a solution that is finite at  is
given by
For a general value of
is
given by
For a general value of  , Equation (117) suggests that a solution may be expanded in a series of
hypergeometric functions with
, Equation (117) suggests that a solution may be expanded in a series of
hypergeometric functions with  being a kind of expansion parameter. This idea was extensively
developed by Leaver [64
being a kind of expansion parameter. This idea was extensively
developed by Leaver [64 ]. Leaver obtained solutions of the Teukolsky equation expressed in a series of
the Coulomb wave functions. The MST formalism is an elegant reformulation of the one by
Leaver [64
]. Leaver obtained solutions of the Teukolsky equation expressed in a series of
the Coulomb wave functions. The MST formalism is an elegant reformulation of the one by
Leaver [64 ].
].
The essential point is to introduce the so-called renormalized angular momentum  , which is a
generalization of
, which is a
generalization of  , to a non-integer value such that the Teukolsky equation admits a solution in a
convergent series of hypergeometric functions. Namely, we add the term
, to a non-integer value such that the Teukolsky equation admits a solution in a
convergent series of hypergeometric functions. Namely, we add the term ![[ν(ν + 1) − λ − s(s + 1)]pin](article512x.gif) to
both sides of Equation (117) to rewrite it as
to
both sides of Equation (117) to rewrite it as
Of course, no modification is done to the original equation, and  is just an irrelevant parameter at
this stage. A trick is to consider the right-hand side of the above equation as a perturbation,
and look for a formal solution specified by the index
is just an irrelevant parameter at
this stage. A trick is to consider the right-hand side of the above equation as a perturbation,
and look for a formal solution specified by the index  in a series expansion form. Then,
only after we obtain the formal solution, we require that the series should converge, and this
requirement determines the value of
in a series expansion form. Then,
only after we obtain the formal solution, we require that the series should converge, and this
requirement determines the value of 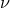 . Note that, if we take the limit
. Note that, if we take the limit  , we must
have
, we must
have  (or
(or  ) to assure
) to assure ![[ν (ν + 1) − λ − s(s + 1)] → 0](article520x.gif) and to recover the
solution (118).
and to recover the
solution (118).
Let us denote the formal solution specified by a value of 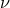 by
by  . We express it in the series form,
. We express it in the series form,
Here, the hypergeometric functions  satisfy the recurrence relations [68
satisfy the recurrence relations [68 ],
Inserting the series (120) into Equation (119) and using the above recurrence relations, we
obtain a three-term recurrence relation among the expansion coefficients
],
Inserting the series (120) into Equation (119) and using the above recurrence relations, we
obtain a three-term recurrence relation among the expansion coefficients  . It is given by
where
The convergence of the series (120) is determined by the asymptotic behaviors of the coefficients
. It is given by
where
The convergence of the series (120) is determined by the asymptotic behaviors of the coefficients  at
at
 . We thus discuss properties of the three-term recurrence relation (123) and the role of the
parameter
. We thus discuss properties of the three-term recurrence relation (123) and the role of the
parameter  in detail.
in detail.
The general solution of the recurrence relation (123) is expressed in terms of two linearly
independent solutions 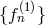 and
and  (
(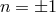 ,
,  ). According to the theory of
three-term recurrence relations (see [49
). According to the theory of
three-term recurrence relations (see [49 ], Page 31) when there exists a pair of solutions that satisfy
], Page 31) when there exists a pair of solutions that satisfy
then the solution  is called minimal as
is called minimal as  (
(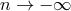 ). Any non-minimal solution is called
dominant. The minimal solution (either as
). Any non-minimal solution is called
dominant. The minimal solution (either as  or as
or as  ) is determined uniquely up to an
overall normalization factor.
) is determined uniquely up to an
overall normalization factor.
The three-term recurrence relation is closely related to continued fractions. We introduce
We can express  and
and 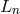 in terms of continued fractions as
These expressions for
in terms of continued fractions as
These expressions for  and
and  are valid if the respective continued fractions converge. It is proved
(see [49
are valid if the respective continued fractions converge. It is proved
(see [49 ], Page 31) that the continued fraction (127) converges if and only if the recurrence relation (123)
possesses a minimal solution as
], Page 31) that the continued fraction (127) converges if and only if the recurrence relation (123)
possesses a minimal solution as  , and the same for the continued fraction (128) as
, and the same for the continued fraction (128) as
 .
.
Analysis of the asymptotic behavior of (123) shows that, as long as  is finite, there exists a set of two
independent solutions that behave as (see, e.g., [49], Page 35)
is finite, there exists a set of two
independent solutions that behave as (see, e.g., [49], Page 35)
and another set of two independent solutions that behave as
Thus,  is minimal as
is minimal as 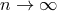 and
and  is minimal as
is minimal as  .
.
Since the recurrence relation (123) possesses minimal solutions as 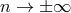 , the continued fractions
on the right-hand sides of Equations (127) and (128) converge for
, the continued fractions
on the right-hand sides of Equations (127) and (128) converge for 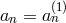 and
and  . In general,
however,
. In general,
however,  and
and  do not coincide. Here, we use the freedom of
do not coincide. Here, we use the freedom of  to obtain a consistent solution.
Let
to obtain a consistent solution.
Let  be a sequence that is minimal for both
be a sequence that is minimal for both  . We then have expressions for
. We then have expressions for  and
and
 in terms of continued fractions as
in terms of continued fractions as
This implies
Thus, if we choose  such that it satisfies the implicit equation for
such that it satisfies the implicit equation for  , Equation (133), for a certain
, Equation (133), for a certain  ,
we obtain a unique minimal solution
,
we obtain a unique minimal solution  that is valid over the entire range of
that is valid over the entire range of  ,
,  , that
is
Note that if Equation (133) for a certain value of
, that
is
Note that if Equation (133) for a certain value of  is satisfied, it is automatically satisfied for any other
value of
is satisfied, it is automatically satisfied for any other
value of  .
.
The minimal solution is also important for the convergence of the series (120). For the minimal solution
 , together with the properties of the hypergeometric functions
, together with the properties of the hypergeometric functions  for large
for large  , we find
, we find
Thus, the series of hypergeometric functions (120) converges for all  in the range
in the range  (in fact,
for all complex values of
(in fact,
for all complex values of  except at
except at  ), provided that the coefficients are given by the minimal
solution.
), provided that the coefficients are given by the minimal
solution.
Instead of Equation (133), we may consider an equivalent but practically more convenient form
of an equation that determines the value of  . Dividing Equation (123) by
. Dividing Equation (123) by 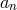 , we find
, we find
where  and
and  are those given by the continued fractions (131) and (132), respectively.
Although the value of
are those given by the continued fractions (131) and (132), respectively.
Although the value of  in this equation is arbitrary, it is convenient to set
in this equation is arbitrary, it is convenient to set  to solve for
to solve for
 .
.
For later use, we need a series expression for  with better convergence properties at large
with better convergence properties at large  .
Using analytic properties of hypergeometric functions, we have
.
Using analytic properties of hypergeometric functions, we have
where
This expression explicitly exhibits the symmetry of  under the interchange of
under the interchange of  and
and  . This
is a result of the fact that
. This
is a result of the fact that  is invariant under the interchange
is invariant under the interchange  . Accordingly, the
recurrence relation (123) has the structure that
. Accordingly, the
recurrence relation (123) has the structure that  satisfies the same recurrence relation as
satisfies the same recurrence relation as
 .
.
Finally, we note that if  is a solution of Equation (133) or (136),
is a solution of Equation (133) or (136),  with an arbitrary
integer
with an arbitrary
integer  is also a solution, since
is also a solution, since  appears only in the combination of
appears only in the combination of  . Thus,
Equation (133) or (136) contains an infinite number of roots. However, not all of these can be used to
express a solution we want. As noted in the earlier part of this section, in order to reproduce the
solution in the limit
. Thus,
Equation (133) or (136) contains an infinite number of roots. However, not all of these can be used to
express a solution we want. As noted in the earlier part of this section, in order to reproduce the
solution in the limit  , Equation (118), we must have
, Equation (118), we must have  (or
(or  by
symmetry). Thus, we impose a constraint on
by
symmetry). Thus, we impose a constraint on  such that it must continuously approach
such that it must continuously approach  as
as
 .
.
![]() , and one irregular singularity at
, and one irregular singularity at
![]() . This implies that it cannot be represented in the form of a single hypergeometric equation.
However, if we focus on the solution near the horizon, it may be approximated by a hypergeometric
equation. This motivates us to consider the solution expressed in terms of a series of hypergeometric
functions.
. This implies that it cannot be represented in the form of a single hypergeometric equation.
However, if we focus on the solution near the horizon, it may be approximated by a hypergeometric
equation. This motivates us to consider the solution expressed in terms of a series of hypergeometric
functions.
![]() in place of
in place of ![]() (
(![]() ) as
) as ![]() , which is a
generalization of
, which is a
generalization of ![]() , to a non-integer value such that the Teukolsky equation admits a solution in a
convergent series of hypergeometric functions. Namely, we add the term
, to a non-integer value such that the Teukolsky equation admits a solution in a
convergent series of hypergeometric functions. Namely, we add the term ![]() to
both sides of Equation (117
to
both sides of Equation (117![]() ) to rewrite it as
) to rewrite it as ![]() by
by ![]() . We express it in the series form,
. We express it in the series form,
![]() ) is expressed in terms of two linearly
independent solutions
) is expressed in terms of two linearly
independent solutions ![]() and
and ![]() (
(![]() ,
, ![]() ). According to the theory of
three-term recurrence relations (see [49
). According to the theory of
three-term recurrence relations (see [49![]() ], Page 31) when there exists a pair of solutions that satisfy
], Page 31) when there exists a pair of solutions that satisfy
![]() ) shows that, as long as
) shows that, as long as ![]() is finite, there exists a set of two
independent solutions that behave as (see, e.g., [49], Page 35)
is finite, there exists a set of two
independent solutions that behave as (see, e.g., [49], Page 35) ![]() is minimal as
is minimal as ![]() and
and ![]() is minimal as
is minimal as ![]() .
.
![]() ) possesses minimal solutions as
) possesses minimal solutions as ![]() , the continued fractions
on the right-hand sides of Equations (127
, the continued fractions
on the right-hand sides of Equations (127![]() ) and (128
) and (128![]() ) converge for
) converge for ![]() and
and ![]() . In general,
however,
. In general,
however, ![]() and
and ![]() do not coincide. Here, we use the freedom of
do not coincide. Here, we use the freedom of ![]() to obtain a consistent solution.
Let
to obtain a consistent solution.
Let ![]() be a sequence that is minimal for both
be a sequence that is minimal for both ![]() . We then have expressions for
. We then have expressions for ![]() and
and
![]() in terms of continued fractions as
in terms of continued fractions as ![]() ). For the minimal solution
). For the minimal solution
![]() , together with the properties of the hypergeometric functions
, together with the properties of the hypergeometric functions ![]() for large
for large ![]() , we find
, we find
![]() ), we may consider an equivalent but practically more convenient form
of an equation that determines the value of
), we may consider an equivalent but practically more convenient form
of an equation that determines the value of ![]() . Dividing Equation (123
. Dividing Equation (123![]() ) by
) by ![]() , we find
, we find
![]() with better convergence properties at large
with better convergence properties at large ![]() .
Using analytic properties of hypergeometric functions, we have
.
Using analytic properties of hypergeometric functions, we have ![]() is a solution of Equation (133
is a solution of Equation (133![]() ) or (136
) or (136![]() ),
), ![]() with an arbitrary
integer
with an arbitrary
integer ![]() is also a solution, since
is also a solution, since ![]() appears only in the combination of
appears only in the combination of ![]() . Thus,
Equation (133
. Thus,
Equation (133![]() ) or (136
) or (136![]() ) contains an infinite number of roots. However, not all of these can be used to
express a solution we want. As noted in the earlier part of this section, in order to reproduce the
solution in the limit
) contains an infinite number of roots. However, not all of these can be used to
express a solution we want. As noted in the earlier part of this section, in order to reproduce the
solution in the limit ![]() , Equation (118
, Equation (118![]() ), we must have
), we must have ![]() (or
(or ![]() by
symmetry). Thus, we impose a constraint on
by
symmetry). Thus, we impose a constraint on ![]() such that it must continuously approach
such that it must continuously approach ![]() as
as
![]() .
.