Rotating Stars in Numerical Relativity

4 Rotating Stars in Numerical Relativity

Recently, the dynamical evolution of rapidly rotating stars has become possible in numerical relativity. In the framework of the 3+1 split of the Einstein equations [283 ], a stationary axisymmetric star can be described by a metric of the standard form

where $α$ is the lapse function, $βi$ is the shift three-vector, and $γij$ is the spatial three-metric, with $i = 1 ...3$ . The spacetime has the following properties:

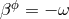The metric function $ω$ in (5 ) describing the dragging of inertial frames by rotation is related to the shift vector through $ϕ β = − ω$ . This shift vector satisfies the minimal distortion shift condition.
The metric satisfies the maximal slicing condition, while the lapse function is related to the metric function $ν$ in (5 ) through $α = eν$ .
The quasi-isotropic coordinates are suitable for numerical evolution, while the radial-gauge coordinates [25 ] are not suitable for nonspherical sources (see [47 ] for details).
The ZAMOs are the Eulerian observers, whose worldlines are normal to the t = const. hypersurfaces.
Uniformly rotating stars have $Ω = const.$ in the coordinate frame. This can be shown by requiring a vanishing rate of shear.
Normal modes of pulsation are discrete in the coordinate frame and their frequencies can be obtained by Fourier transforms (with respect to coordinate time $t$ ) of evolved variables at a fixed coordinate location [106 ].

Crucial ingredients for the successful long-term evolutions of rotating stars in numerical relativity are the conformal ADM schemes for the spacetime evolution (see [233 , 275 , 28 , 4 ]) and hydrodynamical schemes that have been shown to preserve well the sharp rotational profile at the surface of the star [106 , 293 , 105 ].

4.1 Numerical evolution of equilibrium models
  4.1.1 Stable equilibrium
  4.1.2 Instability to collapse
  4.1.3 Dynamical bar-mode instability
4.2 Pulsations of rotating stars
4.3 Rotating core collapse
  4.3.1 Collapse to a rotating black hole
  4.3.2 Formation of rotating neutron stars