3.1 Singularities in spatially homogeneous cosmologies
The generic singularity in spatially
homogeneous cosmologies is reasonably well understood. The approach to it asymptotically falls into two
classes. The first, called asymptotically velocity term dominated (AVTD) [95, 164 ], refers to a cosmology
that approaches the Kasner (vacuum, Bianchi I) solution [171
], refers to a cosmology
that approaches the Kasner (vacuum, Bianchi I) solution [171 ] as
] as 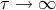 . (Spatially homogeneous
universes can be described as a sequence of homogeneous spaces labeled by
. (Spatially homogeneous
universes can be described as a sequence of homogeneous spaces labeled by  . Here we shall choose
. Here we shall choose 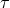 so
that
so
that 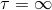 coincides with the singularity.) An example of such a solution is the vacuum Bianchi II
model [236
coincides with the singularity.) An example of such a solution is the vacuum Bianchi II
model [236 ] which begins with a fixed set of Kasner-like anisotropic expansion rates, and, possibly, makes
one change of the rates in a prescribed way (Mixmaster-like bounce) and then continues to
] which begins with a fixed set of Kasner-like anisotropic expansion rates, and, possibly, makes
one change of the rates in a prescribed way (Mixmaster-like bounce) and then continues to
 as a fixed Kasner solution. In contrast are the homogeneous cosmologies which display
Mixmaster dynamics such as vacuum Bianchi VIII and IX [22
as a fixed Kasner solution. In contrast are the homogeneous cosmologies which display
Mixmaster dynamics such as vacuum Bianchi VIII and IX [22 , 187
, 187 , 133] and Bianchi VI
, 133] and Bianchi VI and
Bianchi I with a magnetic field [178
and
Bianchi I with a magnetic field [178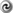 , 26
, 26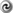 , 177
, 177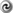 ]. Jantzen [168
]. Jantzen [168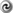 ] has discussed other examples.
Mixmaster dynamics describes an approach to the singularity which is a sequence of Kasner
epochs with a prescription, originally due to Belinskii, Khalatnikov, and Lifshitz (BKL) [22
] has discussed other examples.
Mixmaster dynamics describes an approach to the singularity which is a sequence of Kasner
epochs with a prescription, originally due to Belinskii, Khalatnikov, and Lifshitz (BKL) [22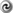 ], for
relating one Kasner epoch to the next. Some of the Mixmaster bounces (era changes) display
sensitivity to initial conditions one usually associates with chaos, and in fact Mixmaster dynamics is
chaotic [85
], for
relating one Kasner epoch to the next. Some of the Mixmaster bounces (era changes) display
sensitivity to initial conditions one usually associates with chaos, and in fact Mixmaster dynamics is
chaotic [85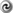 , 194
, 194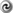 ]. Note that we consider an epoch to be a subunit of an era. In some of the literature, this
usage is reversed. The vacuum Bianchi I (Kasner) solution is distinguished from the other
Bianchi types in that the spatial scalar curvature
]. Note that we consider an epoch to be a subunit of an era. In some of the literature, this
usage is reversed. The vacuum Bianchi I (Kasner) solution is distinguished from the other
Bianchi types in that the spatial scalar curvature  , (proportional to) the minisuperspace
(MSS) potential [187
, (proportional to) the minisuperspace
(MSS) potential [187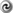 , 227
, 227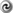 ], vanishes identically. But
], vanishes identically. But  arises in other Bianchi types due
to spatial dependence of the metric in a coordinate basis. Thus an AVTD singularity is also
characterized as a regime in which terms containing or arising from spatial derivatives no longer
influence the dynamics. This means that the Mixmaster models do not have an AVTD singularity
since the influence of the spatial derivatives (through the MSS potential) never disappears
– there is no last bounce. A more general review of numerical cosmology has been given by
Anninos [4].
arises in other Bianchi types due
to spatial dependence of the metric in a coordinate basis. Thus an AVTD singularity is also
characterized as a regime in which terms containing or arising from spatial derivatives no longer
influence the dynamics. This means that the Mixmaster models do not have an AVTD singularity
since the influence of the spatial derivatives (through the MSS potential) never disappears
– there is no last bounce. A more general review of numerical cosmology has been given by
Anninos [4].