4.1 Cosmic microwave background 

The Cosmic Microwave Background Radiation (CMBR), which is a direct relic of the early Universe, currently provides the deepest probe of cosmological structures and imposes severe constraints on the various proposed matter evolution scenarios and cosmological parameters. Although the CMBR is a unique and deep probe of both the thermal history of the early Universe and the primordial perturbations in the matter distribution, the associated anisotropies are not exclusively primordial in nature. Important modifications to the CMBR spectrum can arise from large scale coherent structures, even well after the photons decouple from the matter at redshift 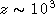, due to the gravitational redshifting of the photons through the Sachs-Wolfe effect arising from potential gradients [111, 13]

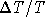where the integral is evaluated from the emission (e) to reception (r) points along the spatial photon paths , is the gravitational potential, defines the temperature fluctuations, and a(t) is the cosmological scale factor in the standard FLRW metric. Also, if the intergalactic medium (IGM) reionizes sometime after the decoupling, say from an early generation of stars, the increased rate of Thomson scattering off the free electrons will erase sub-horizon scale temperature anisotropies, while creating secondary Doppler shift anisotropies. To make meaningful comparisons between numerical models and observed data, these effects (and others, see for example § 4.1.3 and references [79, 82]) must be incorporated self-consistently into the numerical models and to high accuracy in order to resolve the weak signals.

4.1.1 Ray-tracing 

Many computational analyses based on linear perturbation theory have been carried out to estimate the temperature anisotropies in the sky (for example see [92] and the references cited in [79]). Although such linearized approaches yield reasonable results, they are not well-suited to discussing the expected imaging of the developing nonlinear structures in the microwave background. An alternative ray-tracing approach has been developed by Anninos et al. [13] to introduce and propagate individual photons through the evolving nonlinear matter structures. They solve the geodesic equations of motion and subject the photons to Thomson scattering in a probabilistic way and at a rate determined by the local density of free electrons in the model. Since the temperature fluctuations remain small, the equations of motion for the photons are treated as in the linearized limit, and the anisotropies are computed according to

where

and the photon wave vector and matter rest frame four-velocity are evaluated at the emission (e) and reception (r) points. Applying their procedure to a Hot Dark Matter (HDM) model of structure formation, Anninos et al. [13] find the parameters for this model are severely constrained by COBE data such that , where and h are the density and Hubble parameters.

4.1.2 Effects of reionization 

In models where the IGM does not reionize, the probability of scattering after the photon-matter decoupling epoch is low, and the Sachs-Wolfe effect dominates the anisotropies at angular scales larger than a few degrees. However, if reionization occurs, the scattering probability increases substantially and the matter structures, which develop large bulk motions relative to the comoving background, induce Doppler shifts on the scattered CMBR photons and leave an imprint of the surface of last scattering. The induced fluctuations on subhorizon scales in reionization scenarios can be a significant fraction of the primordial anisotropies, as observed by Tuluie et al. [122]. They considered two possible scenarios of reionization: A model that suffers early and gradual (EG) reionization of the IGM as caused by the photoionizing UV radiation emitted by decaying neutrinos, and the late and sudden (LS) scenario as might be applicable to the case of an early generation of star formation activity at high redshifts. Considering the HDM model with and h=0.55, which produces CMBR anisotropies above current COBE limits when no reionization is included (see § 4.1.1), they find that the EG scenario effectively reduces the anisotropies to the levels observed by COBE and generates smaller Doppler shift anisotropies than the LS model, as demonstrated in Figure 4. The LS scenario of reionization is not able to reduce the anisotropy levels below the COBE limits, and can even give rise to greater Doppler shifts than expected at decoupling.

  

Figure 4: The top two images represent temperature fluctuations (i.e., 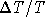) due to the Sachs-Wolfe effect and Doppler shifts in a standard critically closed HDM model with no reionization and baryon fractions 0.02 (plate 1: , rms ) and 0.2 (plate 2: , rms ). The bottom two plates image fluctuations in an ``early and gradual'' reionization scenario of decaying neutrinos with baryon fraction 0.02 (plate 3: , rms 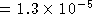; and plate 4: , rms ).

4.1.3 Secondary anisotropies 

Additional sources of CMBR anisotropy can arise from the interactions of photons with dynamically evolving matter structures and nonstatic gravitational potentials. Tuluie et al. [121] considered the impact of nonlinear matter condensations on the CMBR in 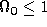Cold Dark Matter (CDM) models, focusing on the relative importance of secondary temperature anisotropies due to three different effects: 1) time-dependent variations in the gravitational potential of nonlinear structures as a result of collapse or expansion (the Rees-Sciama effect); 2) proper motion of nonlinear structures such as clusters and superclusters across the sky; and 3) the decaying gravitational potential effect from the evolution of perturbations in open models. They applied the ray-tracing procedure of [13] to explore the relative importance of these secondary anisotropies as a function of the density parameter and the scale of matter distributions. They find that secondary temperature anisotropies are dominated by the decaying potential effect at large scales, but that all three sources of anisotropy can produce signatures of order as shown in Figure 5.

  

Figure 5: The top two images represent the proper motion and Rees-Sciama effects in the CMBR for a critically closed CDM model (upper left), together with the corresponding column density of voids and clusters over the same region (upper right). The bottom two images show the secondary anisotropies dominated here by the decaying potential effect in an open cosmological model (bottom left), together with the corresponding gravitational potential over the same region (bottom right). The rms fluctuations in both cases are on the order of , though the open model carries a somewhat larger signature.

In addition to the effects discussed here, many other sources of secondary anisotropies (such as gravitational lensing, the Vishniac effect accounting for matter velocities and flows into local potential wells, and the Sunyaev-Zel'dovich (§ 4.5.4) distortions from the Compton scattering of CMB photons by electrons in the hot cluster medium) can also be significant. See reference [79] for a more complete list and thorough discussion of the different sources of CMBR anisotropies.

Computational Cosmology: from the Early Universe to the Large Scale Structure Peter Anninos http://www.livingreviews.org/lrr-2001-2 © Max-Planck-Gesellschaft. ISSN 1433-8351 Problems/Comments to livrev@aei-potsdam.mpg.de