Killing horizons

4.1 Killing horizons

The black hole region of an asymptotically flat spacetime $(M, g )$ is the part of $M$ which is not contained in the causal past of future null infinity.³⁰ Hence, the event horizon, being defined as the boundary of the black hole region, is a global concept. Of crucial importance to the theory of black holes is the strong rigidity theorem, which implies that the event horizon of a stationary spacetime is a Killing horizon.³¹ The definition of the latter is of purely local nature: Consider a Killing field $ξ$ , say, and the set of points where $ξ$ is null, $N ≡ (ξ, ξ) = 0$ . 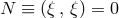A connected component of this set which is a null hyper-surface, $(dN , dN ) = 0$ , is called a Killing horizon, $H [ξ]$ . Killing horizons possess a variety of interesting properties:³²

An immediate consequence of the above definition is the fact that $ξ$ and $dN$ are proportional on $H [ξ]$ . (Note that $(ξ , dN ) = 0$ , since $L ξN = 0$ , and that two orthogonal null vectors are proportional.) This suggests the following definition of the surface gravity, $κ$ ,

Since the Killing equation implies $dN = − 2 ∇ ξξ$ , the above definition shows that the surface gravity measures the extent to which the parametrization of the geodesic congruence generated by $ξ$ is not affine.
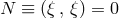A theorem due to Vishveshwara [172 ] gives a characterization of the Killing horizon $H [ξ ]$ in terms of the twist $ω$ of $ξ$ :³³ The surface $N ≡ (ξ, ξ) = 0$ is a Killing horizon if and only if
Using general identities for Killing fields³⁴ one can derive the following explicit expressions for $κ$ :

Introducing the four velocity $√ ---- u = ξ∕ − N$ for a time-like $ξ$ , the first expression shows that the surface gravity is the limiting value of the force applied at infinity to keep a unit mass at $H [ξ]$ in place: $√ ---- κ = lim ( − N |a|)$ , where $a = ∇uu$ (see, e.g. [177 ]).
Of crucial importance to the zeroth law of black hole physics (to be discussed below) is the fact that the $(ξξ)$ -component of the Ricci tensor vanishes on the horizon,

This follows from the above expressions for $κ$ and the general Killing field identity $2N R (ξ,ξ) = 4(∇ ξξ, ∇ ξξ ) − N ΔN − 4(ω , ω )$ .

It is an interesting fact that the surface gravity plays a similar role in the theory of stationary black holes as the temperature does in ordinary thermodynamics. Since the latter is constant for a body in thermal equilibrium, the result

is usually called the zeroth law of black hole physics [3

]. The zeroth law can be established by different means: Each of the following alternatives is sufficient to prove that $κ$ is uniform over the Killing horizon generated by $ξ$ .

(i) Einstein’s equations are fulfilled with matter satisfying the dominant energy condition.

(ii) The domain of outer communications is either static or circular.

(iii) $H [ξ]$ is a bifurcate Killing horizon.

(i) The original proof of the zeroth law rests on the first assumption [3 ]. The reasoning is as follows: First, Einstein’s equations and the fact that $R (ξ,ξ)$ vanishes on the horizon (see above), imply that $T (ξ,ξ) = 0$ on $H [ξ]$ . Hence, the one-form $T (ξ)$ ³⁵ is perpendicular to $ξ$ and, therefore, space-like or null on $H [ξ]$ . On the other hand, the dominant energy condition requires that $T(ξ)$ is time-like or null. Thus, $T(ξ)$ is null on the horizon. Since two orthogonal null vectors are proportional, one has, using Einstein’s equations again, $ξ ∧ R (ξ ) = 0$ on $H [ξ]$ . The result that $κ$ is uniform over the horizon now follows from the general property³⁶

(ii) By virtue of Eq. (6 ) and the general Killing field identity $dω = ∗[ξ ∧ R (ξ)]$ , the zeroth law follows if one can show that the twist one-form is closed on the horizon [147 ]:

While the original proof (i) takes advantage of Einstein’s equations and the dominant energy condition to conclude that the twist is closed, one may also achieve this by requiring that $ω$ vanishes identically,³⁷ which then proves the second version of the first zeroth law.³⁸

(iii) The third version of the zeroth law, due to Kay and Wald [105 ], is obtained for bifurcate Killing horizons. Computing the derivative of the surface gravity in a direction tangent to the bifurcation surface shows that $κ$ cannot vary between the null-generators. (It is clear that $κ$ is constant along the generators.) The bifurcate horizon version of the zeroth law is actually the most general one: First, it involves no assumptions concerning the matter fields. Second, the work of Rácz and Wald strongly suggests that all physically relevant Killing horizons are either of bifurcate type or degenerate [146 , 147 ].