3.3 Higher-order correlation functions
One of the most direct methods to evaluate the deviation from Gaussianity is to compute the
higher-order correlation functions. Suppose that  now labels the position of the
now labels the position of the 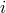 -th object (galaxy).
Then the two-point correlation function
-th object (galaxy).
Then the two-point correlation function 
 is defined also in terms of the
joint probability of the pair of objects located in the volume elements of
is defined also in terms of the
joint probability of the pair of objects located in the volume elements of  and
and  ,
where
,
where  is the mean number density of the objects. This definition is generalized to three- and four-point
correlation functions,
is the mean number density of the objects. This definition is generalized to three- and four-point
correlation functions,  and
and 
 , in a straightforward manner:
Apparently
, in a straightforward manner:
Apparently  ,
,  , and
, and  are symmetric with respect to the change of the indices. Define the
following quantities with the same symmetry properties:
Then it is not unreasonable to suspect that the following relations hold:
where
are symmetric with respect to the change of the indices. Define the
following quantities with the same symmetry properties:
Then it is not unreasonable to suspect that the following relations hold:
where  ,
,  ,
,  , and
, and  are constants. In fact, the analysis of the two-dimensional galaxy
catalogues [68] revealed
The generlization of those relations for
are constants. In fact, the analysis of the two-dimensional galaxy
catalogues [68] revealed
The generlization of those relations for  -point correlation functions is suspected to hold generally,
and is called the hierarchical clustering ansatz. Cosmological
-point correlation functions is suspected to hold generally,
and is called the hierarchical clustering ansatz. Cosmological  -body simulations approximately support
the validity of the above ansatz, but also detect the finite deviation from it [82
-body simulations approximately support
the validity of the above ansatz, but also detect the finite deviation from it [82 ].
].