 |
Figure 1:
2D surface of equilibrium models for EOS L. The surface is bounded by the nonrotating
( ) and mass-shedding ( ) and mass-shedding ( ) limits and formed by constant ) limits and formed by constant  and constant and constant  sequences (solid lines). The projection of these sequences in the
sequences (solid lines). The projection of these sequences in the  – – plane are shown as
long-dashed lines. Also shown are the axisymmetric instability sequence (short-dashed line). The
projection of the 2D surface in the plane are shown as
long-dashed lines. Also shown are the axisymmetric instability sequence (short-dashed line). The
projection of the 2D surface in the  – – plane shows an overlapping (see dotted lines). (Figure 7
of Stergioulas and Friedman [294].) plane shows an overlapping (see dotted lines). (Figure 7
of Stergioulas and Friedman [294].) |
 |
Figure 2:
Iso-energy density lines of a differentially rotating proto-neutron star at the mass-shedding
limit, of rest mass  . (Figure 5a of Goussard, Haensel and Zdunik [135]; used with
permission.) . (Figure 5a of Goussard, Haensel and Zdunik [135]; used with
permission.) |
 |
Figure 3:
Meridional plane cross section of a rapidly rotating strange star at the mass-shedding limit,
obtained with a multi-domain spectral code. The various lines are isocontours of the log-enthalpy
H, as defined in [133]. Solid lines indicate a positive value of H and dashed lines a negative value
(vacuum). The thick solid line denotes the stellar surface. The thick dot-dashed line denotes the
boundary between the two computational domains. (Figure 4 of Gourgoulhon, Haensel, Livine,
Paluch, Bonazzola, and Marck [133]; used with permission.) |
 |
Figure 4:
Apparent intersection (due to avoided crossing) of the axisymmetric first quasi-radial
overtone (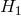 ) and the first overtone of the ) and the first overtone of the  p-mode (in the Cowling approximation).
Frequencies are normalized by p-mode (in the Cowling approximation).
Frequencies are normalized by 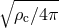 , where , where  is the central energy density of the star. The
rotational frequency is the central energy density of the star. The
rotational frequency  at the mass-shedding limit is 0.597 (in the above units). Along continuous
sequences of computed frequencies, mode eigenfunctions are exchanged at the avoided crossing.
Defining quasi-normal mode sequences by the shape of their eigenfunction, the at the mass-shedding limit is 0.597 (in the above units). Along continuous
sequences of computed frequencies, mode eigenfunctions are exchanged at the avoided crossing.
Defining quasi-normal mode sequences by the shape of their eigenfunction, the  sequence
(filled boxes) appears to intersect with the sequence
(filled boxes) appears to intersect with the  sequence (triangle), but each sequence shows a
discontinuity, when the region of apparent intersection is well resolved. (Figure 3 of Yoshida and
Eriguchi [330]; used with permission.) sequence (triangle), but each sequence shows a
discontinuity, when the region of apparent intersection is well resolved. (Figure 3 of Yoshida and
Eriguchi [330]; used with permission.) |
 |
Figure 5:
Frequencies of several axisymmetric modes along a sequence of rapidly rotating relativistic
polytropes of  , in the Cowling approximation. On the horizontal axis, the angular velocity
of each model is scaled to the angular velocity of the model at the mass-shedding limit. Lower
order modes are weakly affected by rapid rotation, while higher order modes show apparent mode
intersections. (Figure 10 of Font, Dimmelmeier, Gupta, and Stergioulas [104].) , in the Cowling approximation. On the horizontal axis, the angular velocity
of each model is scaled to the angular velocity of the model at the mass-shedding limit. Lower
order modes are weakly affected by rapid rotation, while higher order modes show apparent mode
intersections. (Figure 10 of Font, Dimmelmeier, Gupta, and Stergioulas [104].) |
 |
Figure 6:
Eigenfrequencies (in the Cowling approximation) of f -modes along a 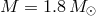 sequence of models, constructed with the WFF3-NV EOS. The vertical line corresponds to the
frequency of rotation of the model at the mass-shedding limit of the sequence. (Figure 1 of Yoshida
and Eriguchi [329]; used with permission.)
sequence of models, constructed with the WFF3-NV EOS. The vertical line corresponds to the
frequency of rotation of the model at the mass-shedding limit of the sequence. (Figure 1 of Yoshida
and Eriguchi [329]; used with permission.) |
 |
Figure 7:
The  neutral f -mode sequences for EOS A. Shown are the ratio of rotational
to gravitational energy neutral f -mode sequences for EOS A. Shown are the ratio of rotational
to gravitational energy  (upper panel) and the ratio of the critical angular velocity (upper panel) and the ratio of the critical angular velocity  to the angular velocity at the mass-shedding limit for uniform rotation (lower panel) as a function
of gravitational mass. The solid curves are the neutral mode sequences for
to the angular velocity at the mass-shedding limit for uniform rotation (lower panel) as a function
of gravitational mass. The solid curves are the neutral mode sequences for  ,
and ,
and  (from top to bottom), while the dashed curve in the upper panel corresponds to the
mass-shedding limit for uniform rotation. The (from top to bottom), while the dashed curve in the upper panel corresponds to the
mass-shedding limit for uniform rotation. The  f -mode becomes CFS-unstable even
at 85% of the mass-shedding limit, for f -mode becomes CFS-unstable even
at 85% of the mass-shedding limit, for  models constructed with this EOS. (Figure 2 of
Morsink, Stergioulas, and Blattning [230].) models constructed with this EOS. (Figure 2 of
Morsink, Stergioulas, and Blattning [230].) |
 |
Figure 8:
Eigenfrequencies (in the Cowling approximation) of the  mode as a function
of the parameter mode as a function
of the parameter  for three different sequences of differentially rotating neutron stars
(the for three different sequences of differentially rotating neutron stars
(the  line corresponding to uniform rotation). The filled circle indicates the neutral
stability point of a uniformly rotating star computed in full general relativity (Stergioulas and
Friedman [295]). Differential rotation shifts the neutral point to higher rotation rates. (Figure 1 of
Yoshida, Rezzolla, Karino, and Eriguchi [333]; used with permission.) line corresponding to uniform rotation). The filled circle indicates the neutral
stability point of a uniformly rotating star computed in full general relativity (Stergioulas and
Friedman [295]). Differential rotation shifts the neutral point to higher rotation rates. (Figure 1 of
Yoshida, Rezzolla, Karino, and Eriguchi [333]; used with permission.) |
 |
Figure 9:
The r-mode instability window for a strange star of  and R =10 km (solid
line). Dashed curves show the corresponding instability windows for normal npe fluid and neutron
stars with a crust. The instability window is compared to i) the inferred spin-periods for accreting
stars in LMBXs [shaded box], and ii) the fastest known millisecond pulsars (for which observational
upper limits on the temperature are available) [horizontal lines]. (Figure 1 of Andersson, Jones, and
Kokkotas [11]; used with permission.) and R =10 km (solid
line). Dashed curves show the corresponding instability windows for normal npe fluid and neutron
stars with a crust. The instability window is compared to i) the inferred spin-periods for accreting
stars in LMBXs [shaded box], and ii) the fastest known millisecond pulsars (for which observational
upper limits on the temperature are available) [horizontal lines]. (Figure 1 of Andersson, Jones, and
Kokkotas [11]; used with permission.) |
 |
Figure 10:
Relativistic r-mode frequencies for a range of the compactness ratio  . The coupling
of polar and axial terms, even in the order . The coupling
of polar and axial terms, even in the order  slow rotation approximation has a dramatic
impact on the continuous frequency bands (shaded areas), allowing the r-mode to exist even in highly
compact stars. The Newtonian value of the r-mode frequency is plotted as a dashed-dotted line.
(Figure 3 of Ruoff, Stavridis, and Kokkotas [257]; used with permission.) slow rotation approximation has a dramatic
impact on the continuous frequency bands (shaded areas), allowing the r-mode to exist even in highly
compact stars. The Newtonian value of the r-mode frequency is plotted as a dashed-dotted line.
(Figure 3 of Ruoff, Stavridis, and Kokkotas [257]; used with permission.) |
 |
Figure 11:
Projected trajectories of several fiducial fluid elements (as seen in the corotating frame)
for an  Newtonian r-mode. All of the fluid elements are initially positioned on the Newtonian r-mode. All of the fluid elements are initially positioned on the
 meridian at different latitudes (indicated with stars). Blue dots indicate the position of the
fluid elements after each full oscillation period. The r-mode induces a kinematical, differential drift.
(Figure 2c of Rezzolla, Lamb, Marković, and Shapiro [252]; used with permission.) meridian at different latitudes (indicated with stars). Blue dots indicate the position of the
fluid elements after each full oscillation period. The r-mode induces a kinematical, differential drift.
(Figure 2c of Rezzolla, Lamb, Marković, and Shapiro [252]; used with permission.) |
 |
Figure 12:
Evolution of the axial velocity in the equatorial plane for a relativistic r-mode in a rapidly
rotating  polytrope (in the Cowling approximation). Since the initial data used to excite
the mode are not exact, the evolution is a superposition of (mainly) the polytrope (in the Cowling approximation). Since the initial data used to excite
the mode are not exact, the evolution is a superposition of (mainly) the  r-mode and
several inertial modes. The amplitude of the oscillation decreases due to numerical (finite-differencing)
viscosity of the code. A beating between the r-mode and
several inertial modes. The amplitude of the oscillation decreases due to numerical (finite-differencing)
viscosity of the code. A beating between the  r-mode and another inertial mode can also
be seen. (Figure 2 of Stergioulas and Font [293].) r-mode and another inertial mode can also
be seen. (Figure 2 of Stergioulas and Font [293].) |
 |
Figure 13:
Time evolution of the rotational velocity profile for a stationary, rapidly rotating
relativistic star (in the Cowling approximation), using the 3rd order PPM scheme and a 1163 grid.
The initial rotational profile is preserved to a high degree of accuracy, even after 20 rotational periods.
(Figure 1 of Stergioulas and Font [293].) |
 |
Figure 14:
(mpg-Movie; 2457 KB)
Movie Simulation of a stationary, rapidly rotating neutron star model in full general relativity,
for 3 rotational periods (shown are iso-density contours, in dimensionless units). The stationary shape
is well preserved at a resolution of 1293. Simulation by Font, Goodale, Iyer, Miller, Rezzolla, Seidel,
Stergioulas, Suen, and Tobias. Visualization by W. Benger and L. Rezzolla at the Albert Einstein
Institute, Golm [1]. |
 |
Figure 15:
Density contours and velocity flow for a neutron star model that has developed spiral
arms, due to the dynamical bar-mode instability. The computation was done in full General Relativity.
(Figure 4 of Shibata, Baumgarte, and Shapiro [273]; used with permission). |
 |
Figure 16:
(mpg-Movie; 1655 KB)
Movie Simulation of the development of the dynamical bar-mode instability in a rapidly rotating
relativistic star. Spiral arms form within a few rotational periods. The different colors correspond
to different values of the density, while the computation was done in full general relativity. Movie
produced at the University of Illinois by T.W. Baumgarte, S.L. Shapiro, and M. Shibata, with the
assistance of the Illinois Undergraduate Research Team [31]; used with permission. |
 |
Figure 17:
(mpg-Movie; 1926 KB)
Movie Gravitational wave emission during the development of the dynamical bar-mode
instability in a rapidly rotating relativistic star. The gravitational wave amplitude in a plane
containing the rotation axis is shown. At large distances, the waves assume a quadrupole-like
angular dependence. Movie produced at the University of Illinois by T.W. Baumgarte, S.L. Shapiro,
and M. Shibata, with the assistance of the Illinois Undergraduate Research Team [31]; used with
permission. |
 |
Figure 18:
The first fully relativistic, quasi-radial pulsation frequencies for a sequence of rapidly
rotating stars (solid lines). The frequencies of the fundamental mode  (filled squares) and of
the first overtone (filled squares) and of
the first overtone  (filled circles) are obtained through coupled hydrodynamical and spacetime
evolutions. The corresponding frequencies obtained from computations in the relativistic Cowling
approximation [104] are shown as dashed lines. (Figure 16 of Font, Goodale, Iyer, Miller, Rezzolla,
Seidel, Stergioulas, Suen, and Tobias [105].) (filled circles) are obtained through coupled hydrodynamical and spacetime
evolutions. The corresponding frequencies obtained from computations in the relativistic Cowling
approximation [104] are shown as dashed lines. (Figure 16 of Font, Goodale, Iyer, Miller, Rezzolla,
Seidel, Stergioulas, Suen, and Tobias [105].) |

















