3.1 Quasi-normal modes of oscillation
A general linear perturbation of the energy density in a static and spherically symmetric relativistic star
can be written as a sum of quasi-normal modes that are characterized by the indices  of
the spherical harmonic functions
of
the spherical harmonic functions  and have angular and time dependence of the form
where
and have angular and time dependence of the form
where  indicates the Eulerian perturbation of a quantity,
indicates the Eulerian perturbation of a quantity,  is the angular frequency of the
mode as measured by a distant inertial observer,
is the angular frequency of the
mode as measured by a distant inertial observer, 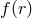 represents the radial dependence of
the perturbation, and
represents the radial dependence of
the perturbation, and  are the associated Legendre polynomials. Normal modes of
nonrotating stars are degenerate in
are the associated Legendre polynomials. Normal modes of
nonrotating stars are degenerate in  and it suffices to study the axisymmetric
and it suffices to study the axisymmetric  case.
case.
The Eulerian perturbation in the fluid 4-velocity  can be expressed in terms of vector harmonics,
while the metric perturbation
can be expressed in terms of vector harmonics,
while the metric perturbation 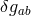 can be expressed in terms of spherical, vector, and tensor
harmonics. These are either of “polar” or “axial” parity. Here, parity is defined to be the change in
sign under a combination of reflection in the equatorial plane and rotation by
can be expressed in terms of spherical, vector, and tensor
harmonics. These are either of “polar” or “axial” parity. Here, parity is defined to be the change in
sign under a combination of reflection in the equatorial plane and rotation by  . A polar
perturbation has parity
. A polar
perturbation has parity  , while an axial perturbation has parity
, while an axial perturbation has parity  . Because of the
spherical background, the polar and axial perturbations of a nonrotating star are completely
decoupled.
. Because of the
spherical background, the polar and axial perturbations of a nonrotating star are completely
decoupled.
A normal mode solution satisfies the perturbed gravitational field equations,
and the perturbation of the conservation of the stress-energy tensor,
with suitable boundary conditions at the center of the star and at infinity. The latter equation is
decomposed into an equation for the perturbation in the energy density  and into equations for the
three spatial components of the perturbation in the 4-velocity
and into equations for the
three spatial components of the perturbation in the 4-velocity  . As linear perturbations have
a gauge freedom, at most six components of the perturbed field equations (49) need to be
considered.
. As linear perturbations have
a gauge freedom, at most six components of the perturbed field equations (49) need to be
considered.
For a given pair  , a solution exists for any value of the frequency
, a solution exists for any value of the frequency  , consisting of a mixture of
ingoing and outgoing wave parts. Outgoing quasi-normal modes are defined by the discrete set of
eigenfrequencies for which there are no incoming waves at infinity. These are the modes that will be excited
in various astrophysical situations.
, consisting of a mixture of
ingoing and outgoing wave parts. Outgoing quasi-normal modes are defined by the discrete set of
eigenfrequencies for which there are no incoming waves at infinity. These are the modes that will be excited
in various astrophysical situations.
The main modes of pulsation that are known to exist in relativistic stars have been classified as follows
( and
and  are typical frequencies and damping times of the most important modes in the nonrotating
limit):
are typical frequencies and damping times of the most important modes in the nonrotating
limit):
- Polar fluid modes are slowly damped modes analogous to the Newtonian fluid pulsations:
- f (undamental)-modes: surface modes due to the interface between the star and its
surroundings (
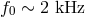 ,
,  ),
),
- p(ressure)-modes: nearly radial (
 ,
,  ),
),
- g(ravity)-modes: nearly tangential, only exist in stars that are non-isentropic or that have
a composition gradient or first order phase transition (
 ,
,  ).
).
- Axial and hybrid fluid modes:
- inertial modes: degenerate at zero frequency in nonrotating stars. In a rotating star, some
inertial modes are generically unstable to the CFS instability; they have frequencies from
zero to kHz and growth times inversely proportional to a high power of the star’s angular
velocity. Hybrid inertial modes have both axial and polar parts even in the limit of no
rotation.
- r(otation)-modes: a special case of inertial modes that reduce to the classical axial r-modes
in the Newtonian limit. Generically unstable to the CFS instability with growth times as
short as a few seconds at high rotation rates.
- Polar and axial spacetime modes:
- w(ave)-modes: Analogous to the quasi-normal modes of a black hole (very weak coupling
to the fluid). High frequency, strongly damped modes (
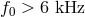 ,
,  ).
).
For a more detailed description of various types of oscillation modes, see [177, 176, 225, 56, 180].
![]() can be expressed in terms of vector harmonics,
while the metric perturbation
can be expressed in terms of vector harmonics,
while the metric perturbation ![]() can be expressed in terms of spherical, vector, and tensor
harmonics. These are either of “polar” or “axial” parity. Here, parity is defined to be the change in
sign under a combination of reflection in the equatorial plane and rotation by
can be expressed in terms of spherical, vector, and tensor
harmonics. These are either of “polar” or “axial” parity. Here, parity is defined to be the change in
sign under a combination of reflection in the equatorial plane and rotation by ![]() . A polar
perturbation has parity
. A polar
perturbation has parity ![]() , while an axial perturbation has parity
, while an axial perturbation has parity ![]() . Because of the
spherical background, the polar and axial perturbations of a nonrotating star are completely
decoupled.
. Because of the
spherical background, the polar and axial perturbations of a nonrotating star are completely
decoupled.
![]() , a solution exists for any value of the frequency
, a solution exists for any value of the frequency ![]() , consisting of a mixture of
ingoing and outgoing wave parts. Outgoing quasi-normal modes are defined by the discrete set of
eigenfrequencies for which there are no incoming waves at infinity. These are the modes that will be excited
in various astrophysical situations.
, consisting of a mixture of
ingoing and outgoing wave parts. Outgoing quasi-normal modes are defined by the discrete set of
eigenfrequencies for which there are no incoming waves at infinity. These are the modes that will be excited
in various astrophysical situations.
![]() and
and ![]() are typical frequencies and damping times of the most important modes in the nonrotating
limit):
are typical frequencies and damping times of the most important modes in the nonrotating
limit):