 |
Figure 1:
A historical time-line showing the major evolutionary stages of our Universe according to
the standard model, from the earliest moments of the Planck era to the present. The horizontal axis
represents logarithmic time in seconds (or equivalently energy in electron-Volts or temperature in
Kelvin), and the solid red line roughly models the radius of the Universe, showing the different rates
of expansion at different times: exponential during inflation, shallow power law during the radiation
dominated era, and a somewhat steeper power law during the current matter dominated phase. |
 |
Figure 2:
Schematic depicting the general sequence of events in the post-recombination Universe.
The solid and dotted lines potentially track the Jeans mass of the average baryonic gas component
from the recombination epoch at  to the current time. A residual ionization fraction
of to the current time. A residual ionization fraction
of  following recombination allows for Compton interactions with photons to following recombination allows for Compton interactions with photons to
 , during which the Jeans mass remains constant at , during which the Jeans mass remains constant at  . The Jeans mass then decreases
as the Universe expands adiabatically until the first collapsed structures form sufficient amounts
of hydrogen molecules to trigger a cooling instability and produce pop III stars at . The Jeans mass then decreases
as the Universe expands adiabatically until the first collapsed structures form sufficient amounts
of hydrogen molecules to trigger a cooling instability and produce pop III stars at  . Star
formation activity can then reheat the Universe and raise the mean Jeans mass to above . Star
formation activity can then reheat the Universe and raise the mean Jeans mass to above  .
This reheating could affect the subsequent development of structures such as galaxies and the
observed Ly .
This reheating could affect the subsequent development of structures such as galaxies and the
observed Ly clouds. clouds. |
 |
Figure 3:
Contour plot of the Bianchi type IX potential  , where , where  are the anisotropy canonical
coordinates. Seven level surfaces are shown at equally spaced decades ranging from 10–1 to 105.
For large isocontours ( are the anisotropy canonical
coordinates. Seven level surfaces are shown at equally spaced decades ranging from 10–1 to 105.
For large isocontours (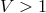 ), the potential is open and exhibits a strong triangular symmetry
with three narrow channels extending to spatial infinity. For ), the potential is open and exhibits a strong triangular symmetry
with three narrow channels extending to spatial infinity. For  , the potential closes and is
approximately circular for , the potential closes and is
approximately circular for  . . |
 |
Figure 4:
Fractal structure of the transition between reflected and captured states for colliding
kink-antikink solitons in the parameter space of impact velocity for a  scalar field
potential. The top image (a) shows the 2-bounce windows in dark with the rightmost region
( scalar field
potential. The top image (a) shows the 2-bounce windows in dark with the rightmost region
( ) representing the single-bounce regime above which no captured state exists, and
the leftmost white region ( ) representing the single-bounce regime above which no captured state exists, and
the leftmost white region ( ) representing the captured state below which no reflection
windows exist. Between these two marker velocities, there are 2-bounce reflection states of decreasing
widths separated by regions of bion formation. Zooming in on the domain outlined by the dashed box,
a self-similar structure is apparent in the middle image (b), where now the dark regions represent
3-bounce windows of decreasing widths. Zooming in once again on the boundaries of these 3-bounce
windows, a similar structure is found as shown in the bottom image (c) but with 4-bounce reflection
windows. This pattern of self-similarity characterized by ) representing the captured state below which no reflection
windows exist. Between these two marker velocities, there are 2-bounce reflection states of decreasing
widths separated by regions of bion formation. Zooming in on the domain outlined by the dashed box,
a self-similar structure is apparent in the middle image (b), where now the dark regions represent
3-bounce windows of decreasing widths. Zooming in once again on the boundaries of these 3-bounce
windows, a similar structure is found as shown in the bottom image (c) but with 4-bounce reflection
windows. This pattern of self-similarity characterized by  -bounce windows is observed at all scales
investigated numerically. -bounce windows is observed at all scales
investigated numerically. |
 |
Figure 5:
Image sequence of the scalar field from a 2D calculation showing the interaction of two
deflagration systems (one planar wall propagating from the right side, and one spherical bubble
nucleating from the center). The physical size of the grid is set to 1000 × 1000 fm and resolved by
512 × 512 zones. The run time of the simulation is about two sound crossing times, where the sound
speed is  , so the shock fronts leading the condensing phase fronts travel across the grid twice.
The hot quark (cold hadron) phases have smaller (larger) scalar field values and are represented by
black (color) in the colormap. , so the shock fronts leading the condensing phase fronts travel across the grid twice.
The hot quark (cold hadron) phases have smaller (larger) scalar field values and are represented by
black (color) in the colormap. |
 |
Figure 6:
Image sequence of the scalar field from a 2D calculation showing the interaction of two
detonation systems (one planar wall propagating from the right side, and one spherical bubble
nucleating from the center). The physical size of the grid is set to 1000 × 1000 fm and resolved by
1024 × 1024 zones. The run time of the simulation is about two sound crossing times. |
 |
Figure 7:
Image sequence of the scalar field from a 2D calculation showing the interaction of shock
and rarefaction waves with a deflagration wall (initiated at the left side) and a detonation wall
(starting from the right). A shock and rarefaction wave travel to the right and left, respectively, from
the temperature discontinuity located initially at the grid center (the right half of the grid is at a
higher temperature). The physical size of the domain is set to 1806.1 × 451.53 fm and resolved by
2048 × 512 zones. The run time of the simulation is about two sound crossing times. |
 |
Figure 8:
Historical time-line of the cosmic microwave background radiation showing the start
of photon/nuclei combination, the surface of last scattering (SoLS), and the epoch of reionization
due to early star formation. The times are represented in years (to the right) and redshift (to
the left). Primary anisotropies are collectively attributed to the early effects at the last scattering
surface and the large scale Sachs–Wolfe effect. Secondary anisotropies arise from path integration
effects, reionization smearing, and higher order interactions with the evolving nonlinear structures
at relatively low redshifts. |
 |
Figure 9:
Temperature fluctuations ( ) in the CMBR due to the primary Sachs–Wolfe
(SW) effect and secondary integrated SW, Doppler, and Thomson scattering effects in a critically
closed model. The top two plates are results with no reionization and baryon fractions 0.02 (plate
1, ) in the CMBR due to the primary Sachs–Wolfe
(SW) effect and secondary integrated SW, Doppler, and Thomson scattering effects in a critically
closed model. The top two plates are results with no reionization and baryon fractions 0.02 (plate
1,  , ,  ), and 0.2 (plate 2, ), and 0.2 (plate 2,  , ,  ).
The bottom two plates are results from an “early and gradual” reionization scenario of decaying
neutrinos with baryon fraction 0.02 (plate 3, ).
The bottom two plates are results from an “early and gradual” reionization scenario of decaying
neutrinos with baryon fraction 0.02 (plate 3,  , ,  ; and plate 4, ; and plate 4,
 , ,  ). If reionization occurs, the scattering probability increases and
anisotropies are damped with each scattering event. At the same time, matter structures develop
large bulk motions relative to the comoving background and induce Doppler shifts on the CMB. The
imprint of this effect from last scattering can be a significant fraction of primary anisotropies. ). If reionization occurs, the scattering probability increases and
anisotropies are damped with each scattering event. At the same time, matter structures develop
large bulk motions relative to the comoving background and induce Doppler shifts on the CMB. The
imprint of this effect from last scattering can be a significant fraction of primary anisotropies. |
 |
Figure 10:
Secondary anisotropies from the proper motion of galaxy clusters across the sky
and Rees–Sciama effects are presented in the upper-left image over  in a critically
closed Cold Dark Matter model. The corresponding column density of matter over the same
region ( in a critically
closed Cold Dark Matter model. The corresponding column density of matter over the same
region ( , ,  ) is displayed in the upper-right, clearly showing the dipolar
nature of the proper motion effect. Anisotropies arising from decaying potentials in an open ) is displayed in the upper-right, clearly showing the dipolar
nature of the proper motion effect. Anisotropies arising from decaying potentials in an open
 model over a scale of model over a scale of  are shown in the bottom left image, along with
the gravitational potential over the same region ( are shown in the bottom left image, along with
the gravitational potential over the same region ( , ,  ) in the bottom right,
demonstrating a clear anti-correlation. Maximum temperature fluctuations in each simulation are ) in the bottom right,
demonstrating a clear anti-correlation. Maximum temperature fluctuations in each simulation are
 respectvely. Secondary anisotropies are dominated by decaying
potentials at large scales, but all three sources (decaying potential, proper motion, and R-S) produce
signatures of order 10–6. respectvely. Secondary anisotropies are dominated by decaying
potentials at large scales, but all three sources (decaying potential, proper motion, and R-S) produce
signatures of order 10–6. |
 |
Figure 11:
Distribution of the gas density at redshift  from a numerical hydrodynamics
simulation of the Ly from a numerical hydrodynamics
simulation of the Ly forest with a CDM spectrum normalized to second year COBE observations,
Hubble parameter of forest with a CDM spectrum normalized to second year COBE observations,
Hubble parameter of  , a comoving box size of 9.6 Mpc, and baryonic density of , a comoving box size of 9.6 Mpc, and baryonic density of  composed of 76% hydrogen and 24% helium. The region shown is 2.4 Mpc (proper) on a side.
The isosurfaces represent baryons at ten times the mean density and are color coded to the gas
temperature (dark blue = 3 × 104 K, light blue = 3 × 105 K). The higher density contours trace
out isolated spherical structures typically found at the intersections of the filaments. A single random
slice through the cube is also shown, with the baryonic overdensity represented by a rainbow-like
color map changing from black (minimum) to red (maximum). The He+ mass fraction is shown with
a wire mesh in this same slice. To emphasize fine structure in the minivoids, the mass fraction in the
overdense regions has been rescaled by the gas overdensity wherever it exceeds unity.
composed of 76% hydrogen and 24% helium. The region shown is 2.4 Mpc (proper) on a side.
The isosurfaces represent baryons at ten times the mean density and are color coded to the gas
temperature (dark blue = 3 × 104 K, light blue = 3 × 105 K). The higher density contours trace
out isolated spherical structures typically found at the intersections of the filaments. A single random
slice through the cube is also shown, with the baryonic overdensity represented by a rainbow-like
color map changing from black (minimum) to red (maximum). The He+ mass fraction is shown with
a wire mesh in this same slice. To emphasize fine structure in the minivoids, the mass fraction in the
overdense regions has been rescaled by the gas overdensity wherever it exceeds unity. |
 |
Figure 12:
Two different model simulations of cosmological sheets are presented: a six species model
including only atomic line cooling (left), and a nine species model including also hydrogen molecules
(right). The evolution sequences in the images show the baryonic overdensity and gas temperature
at three redshifts following the initial collapse at  . In each figure, the vertical axis is 32 kpc
long (parallel to the plane of collapse) and the horizontal axis extends to 4 Mpc on a logarithmic
scale to emphasize the central structures. Differences in the two cases are observed in the cold
pancake layer and the cooling flows between the shock front and the cold central layer. When the
central layer fragments, the thickness of the cold gas layer in the six (nine) species case grows to
3 (0.3) kpc and the surface density evolves with a dominant transverse mode corresponding to a
scale of approximately 8 (1) kpc. Assuming a symmetric distribution of matter along the second
transverse direction, the fragment masses are approximately 107 (105) solar masses. . In each figure, the vertical axis is 32 kpc
long (parallel to the plane of collapse) and the horizontal axis extends to 4 Mpc on a logarithmic
scale to emphasize the central structures. Differences in the two cases are observed in the cold
pancake layer and the cooling flows between the shock front and the cold central layer. When the
central layer fragments, the thickness of the cold gas layer in the six (nine) species case grows to
3 (0.3) kpc and the surface density evolves with a dominant transverse mode corresponding to a
scale of approximately 8 (1) kpc. Assuming a symmetric distribution of matter along the second
transverse direction, the fragment masses are approximately 107 (105) solar masses. |










